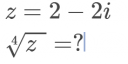Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Komplex számok n-edik gyöke
 onodilevi1
kérdése
onodilevi1
kérdése
426
Az csatolt képen látható a feladat. A fő kérdésem az, hogyan tudom kiszámolni a 4. gyök Z abszolút értékét, ami ugye egyenlő r-el.
Jelenleg 1 felhasználó nézi ezt a kérdést.
analízis, komlexszámok, komplex
analízis, komlexszámok, komplex
0
Felsőoktatás / Matematika
Válaszok
1 gyula205
megoldása
gyula205
megoldása
Két probléma megoldását várod.
1./ Az abszolút értékes problémádat a következő azonosság felhasználásával oldhatod meg:
`abs(root(4)(u+iv))=root(4)(abs(u+iv))=root(4)(r)`. Ez itt `root(4)(sqrt(8))=root(8)(8)` értéket vesz fel.
2./ A csatolt képen látható feladat megoldásához megjegyzem, hogy a negyedik gyök a komplex számok halmazán négy értékű művelet, ami azt jelenti, hogy négy gyököt kell kiszámolni. Meg kell oldani a `z^4-2+2i=0` egyenletet. Ezt tovább alakítva így néz ki: `=(z^2 - sqrt(2 - 2·i))·(z^2 + sqrt(2 - 2·i))=0`, amiből adódik, hogy valójában kétszer két gyökhöz kell eljutni. Mivel `r=sqrt(8)`, ezért a trigonometrikus és az exponenciális alakok felhasználásával könnyebben tudsz gyököt vonni a következő képlet alapján.
`root(n)(z)=root(n)(r)*e^(i(phi/n+2k*pi/n))`, ahol `k=0,1,2` és `3`. Ebben az esetben `n=4`, `r=sqrt(8)` és `phi=-pi/4`.
Tehát a gyökök: `root(8)(8)·e^(- i·l·pi/16)`, ahol `l=1, 9, 17` és `25`.
1./ Az abszolút értékes problémádat a következő azonosság felhasználásával oldhatod meg:
`abs(root(4)(u+iv))=root(4)(abs(u+iv))=root(4)(r)`. Ez itt `root(4)(sqrt(8))=root(8)(8)` értéket vesz fel.
2./ A csatolt képen látható feladat megoldásához megjegyzem, hogy a negyedik gyök a komplex számok halmazán négy értékű művelet, ami azt jelenti, hogy négy gyököt kell kiszámolni. Meg kell oldani a `z^4-2+2i=0` egyenletet. Ezt tovább alakítva így néz ki: `=(z^2 - sqrt(2 - 2·i))·(z^2 + sqrt(2 - 2·i))=0`, amiből adódik, hogy valójában kétszer két gyökhöz kell eljutni. Mivel `r=sqrt(8)`, ezért a trigonometrikus és az exponenciális alakok felhasználásával könnyebben tudsz gyököt vonni a következő képlet alapján.
`root(n)(z)=root(n)(r)*e^(i(phi/n+2k*pi/n))`, ahol `k=0,1,2` és `3`. Ebben az esetben `n=4`, `r=sqrt(8)` és `phi=-pi/4`.
Tehát a gyökök: `root(8)(8)·e^(- i·l·pi/16)`, ahol `l=1, 9, 17` és `25`.
Módosítva: 4 éve
1
- Még nem érkezett komment!