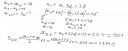Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Számtani Sorozatok
nemtudommmm
kérdése
638
1.)Egy számtani sorozat 1. és 4. tag összege 38, a 7. és 3. tag különbsége 16. Mennyi a 23. tag? S60?
2.) a2+a8=10, a5 x a10=-25. Mennyi a d? mennyi az a1?
3.) Mennyi az 105+110+115+...+1005? Sn=?
4) a1=13, d=17. Hány ötjegyű szám tagja a sorozatnak?
2.) a2+a8=10, a5 x a10=-25. Mennyi a d? mennyi az a1?
3.) Mennyi az 105+110+115+...+1005? Sn=?
4) a1=13, d=17. Hány ötjegyű szám tagja a sorozatnak?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2
Ármós Csaba
megoldása
Szia!
2. feladatra: (a1+d)+(a1+7d)=10, ebből 2×a1+8×d=10, vagyis a1+4d=5, ez pedig az 5. tag lesz pontosan.
a1=(5-4d) egyszer, (a1+4d)×(a1+9d)=-25, ebből pedig 5×(a1+9d)=-25, miből a1+9d=-5, ez meg a 10. tag lesz pontosan, de ez utóbbiból a1=(-5-9d), az előző a1-re felírt kifejezés miatt: (5-4d)=(-5-9d), 5d=2×(-5), amelyből pedig d=2×(-1)=(-2) a differenciája a sorozatnak! a1 pedig ((5-4×(-2))=(5+8)=13 lesz az első tagja a sorozatnak!
3. feladatra: Első tagja 105, utolsó tagja 1005, a differencia (d) meg (110-105)=5 lesz. a(n)=a1 + (n-1)×d képlet miatt behelyettesítéssel 1005=105+(n-1)×5-ből (egyenletből) 900/5=n-1 , miből meg n=180+1=181 az utolsó tag indexe (sorszámja)!
S(n)=(n/2)×((a1+a(n)) képletből behelyettesítéssel: S(n)=(181/2)×(105+1005)=(181×1110)/2=99. 900 lesz az első 181 tag összege ebben a számtani sorozatban!
2. feladatra: (a1+d)+(a1+7d)=10, ebből 2×a1+8×d=10, vagyis a1+4d=5, ez pedig az 5. tag lesz pontosan.
a1=(5-4d) egyszer, (a1+4d)×(a1+9d)=-25, ebből pedig 5×(a1+9d)=-25, miből a1+9d=-5, ez meg a 10. tag lesz pontosan, de ez utóbbiból a1=(-5-9d), az előző a1-re felírt kifejezés miatt: (5-4d)=(-5-9d), 5d=2×(-5), amelyből pedig d=2×(-1)=(-2) a differenciája a sorozatnak! a1 pedig ((5-4×(-2))=(5+8)=13 lesz az első tagja a sorozatnak!
3. feladatra: Első tagja 105, utolsó tagja 1005, a differencia (d) meg (110-105)=5 lesz. a(n)=a1 + (n-1)×d képlet miatt behelyettesítéssel 1005=105+(n-1)×5-ből (egyenletből) 900/5=n-1 , miből meg n=180+1=181 az utolsó tag indexe (sorszámja)!
S(n)=(n/2)×((a1+a(n)) képletből behelyettesítéssel: S(n)=(181/2)×(105+1005)=(181×1110)/2=99. 900 lesz az első 181 tag összege ebben a számtani sorozatban!
1
- Még nem érkezett komment!