1, Ha a területek aránya `16/49` = `4^2/7^2` = `(4/7)^2`, akkor a lineáris méretek aránya `root()((4/7)^2)` = 4:7.

2, Ha a téefogatok aránya `27/125` = `3^3/5^3` = `(3/5)^3`, akkor a lineáris méretek aránya `root(3)((3/5)^3)` = 3:5.

3, A befogótétel kimondja, hogy a derékszögű háromszög befogója mértani közepe az átfogónak és a befogó átfogóra eső merőleges vetületének.

Ha 1:3 arányban osztjuk a 16 cm-es átfogót, akkor az egyik merőleges vetület p =`1*16/(1+3)` = 4 cm, a másik pedig q =`3*16/(1+4)` = 12 cm.

a = `root()(p*c)` = `root()(4*16)` = `root()(64)` = 8 cm

b = `root()(q*c)` = `root()(12*16)` = `root()(192)` = `8*root()(3)` cm `approx` 13,86 cm

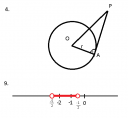
4, Ábra

r = `root()((OP)^2-(OA)^2)` = `root()(17.5^2-14^2)` = 10,5 cm

5,

`sinalpha` = `a/c`

a = `c*sinalpha` = `10.4*sin13` = 2,34 m mély a garázs.

6,

`tan alpha` = `a/b` = `76/38`

`alpha` = 63,43°

7,

`5x^2-6x+1` = `2x^2-x+3`

nullára rendezés

`3x^2-5x-2=0`

`x_(1,2)` = `(5 pm root()(25-4*3*(-2)))/(2*3)` = `(5 pm 7)/6`

`x_1` = `-1/3`

`x_2` = 2

8,

(x-21)(x+3) = 0

`x^2-18x+63=0`

9,

`4x^2+12x+5 lt 0`

megoldjuk, mint egyenletet:

`x_(1,2)` = `(-12pm root()(12^2-4*4*5))/(2*4)` = `(-12pm8)/8`

`x_1` = `-5/2`

`x_2` = `-1/2`

I. Ha `x lt -5/2`, akkor `4x^2+12x+5 gt 0`

II. Ha `-5/2 lt x lt -1/2`, akkor `4x^2+12x+5 lt 0`

III, Ha `x gt `-1/2`, akkor `4x^2+12x+5 gt 0`

Megoldás: `-5/2 lt x lt -1/2`

Ábra