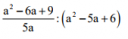Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Tört osztása másodfokú egyenlettel
noxter-norxert1704
kérdése
465
Lehet használni azt a "trükköt", hogy amivel alapból osztanánk, az kvázi egy "tört", csak a nevezője 1, és akkor a reciprokával beszorozzuk a dolgokat?
Ha igen, akkor a nevezőben az lesz, hogy 5a^3 - 25a^2 + 30a , a számláló pedig változatlan.
Ebben az esetben hogyan tovább?
A feladat csak annyit mond, hogy végezzük el a műveleteket a változók lehetséges értékeinél.
Ha igen, akkor a nevezőben az lesz, hogy 5a^3 - 25a^2 + 30a , a számláló pedig változatlan.
Ebben az esetben hogyan tovább?
A feladat csak annyit mond, hogy végezzük el a műveleteket a változók lehetséges értékeinél.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
4
Rantnad
{ 
}
megoldása
Igen, de ne szorozd össze, és akkor 5a*(a²-5a+6) lesz a nevezőben, a feladat pedig ugyanaz marad, mint eddig volt.
0
- Még nem érkezett komment!
noxter-norxert1704
válasza
Vagyis ki kell számolnom a gyökeit a nevezőnek, és utána pedig oda írom, hogy a kapott gyökök értékeinél 0 lenne az egész tehát a nevező is, ami ugyebár nem lehet, tehát x eleme a valós számoknak (R), kivétel az a 2 érték, amit kaptam gyöknek.
A számlálónak is kiszámolom de az nem befolyásolja a kritériumot.
Utána pedig a nevezőnél például a tanult módszer szerint beszorzom az értéket 5a-val, és a kapott 2 gyök előjelét "megcserélem" úgy, hogy: 5a*(x-gyök1)*(x-gyök2) , és tadaaam ?
A számlálónak is kiszámolom de az nem befolyásolja a kritériumot.
Utána pedig a nevezőnél például a tanult módszer szerint beszorzom az értéket 5a-val, és a kapott 2 gyök előjelét "megcserélem" úgy, hogy: 5a*(x-gyök1)*(x-gyök2) , és tadaaam ?
0
-
Rantnad: Igen, tadaaam. 7 éve 1
bongolo
{ }
válasza
Jól gondolod nagy vonalakban, de van pár apróság, ami mind kis hiba:
> utána pedig oda írom, hogy a kapott gyökök értékeinél 0 lenne
> az egész tehát a nevező is
Ne írd oda, hogy "az egész", mert azt félreérthetik. Csak a nevező lenne nulla. (A teljes tört nem, de ezt bizonyára te is így gondolod.)
> x eleme a valós számoknak (R), kivétel az a 2 érték, amit kaptam gyöknek.
Majdnem.
A nevezőnek nem 2, hanem 3 gyöke van. A másodfokú (a²-5a+6)-ból jön 2 gyök, de ott van még az 5a is, ami pedig a=0 esetén nulla, vagyis a 0 is gyök.
És nem x-ről van szó, hanem 'a' a változó neve. Vagyis 'a' eleme a valósaknak, kivéve 0, 2 és 3 (ugyanis a másodfokú két gyöke 2 és 3). Amit így lehet rövidebben leírni:
a ∈ ℝ \ {0, 2, 3}
> A számlálónak is kiszámolom de az nem befolyásolja a kritériumot.
Így van. A számlálót csak azért kell kiszámolni, hogy szorzattá tudjad alakítani. Vagy ha kicsit belegondolsz, kis gyakorlással ránézésre látszik, hogy a számláló éppen (a-3)². De persze teljesen jó az is, ha a megoldóképletet használod.
> a kapott 2 gyök előjelét "megcserélem" úgy, hogy:
> 5a*(x-gyök1)*(x-gyök2)
Így van, de megint: nem x, hanem 'a' a változó neve. Vagyis:
5a · (a-gyök1) · (a-gyök2)
A két gyök 2 és 3, vagyis a nevező 5a(a-2)(a-3).
A tört tehát:
(a-3)² / 5a(a-2)(a-3)
Az (a-3) ott van a számlálóban és a nevezőben is, lehet vele egyszerűsíteni, vagyis ez lesz:
a-3 / 5a(a-2)
És most tadaaam
Megjegyzés:
Most már nincs a nevezőben (a-3), vagyis ez a nevező nem lesz nulla a=3 esetén. Ennek ellenére mivel az eredeti kifejezés nincs értelmezve a=3-nál, továbbra is, ezzel a törttel is az van, hogy a ∈ ℝ \ {0, 2, 3}
Ha bármi nem tiszta, kérdezz rá.
> utána pedig oda írom, hogy a kapott gyökök értékeinél 0 lenne
> az egész tehát a nevező is
Ne írd oda, hogy "az egész", mert azt félreérthetik. Csak a nevező lenne nulla. (A teljes tört nem, de ezt bizonyára te is így gondolod.)
> x eleme a valós számoknak (R), kivétel az a 2 érték, amit kaptam gyöknek.
Majdnem.
A nevezőnek nem 2, hanem 3 gyöke van. A másodfokú (a²-5a+6)-ból jön 2 gyök, de ott van még az 5a is, ami pedig a=0 esetén nulla, vagyis a 0 is gyök.
És nem x-ről van szó, hanem 'a' a változó neve. Vagyis 'a' eleme a valósaknak, kivéve 0, 2 és 3 (ugyanis a másodfokú két gyöke 2 és 3). Amit így lehet rövidebben leírni:
a ∈ ℝ \ {0, 2, 3}
> A számlálónak is kiszámolom de az nem befolyásolja a kritériumot.
Így van. A számlálót csak azért kell kiszámolni, hogy szorzattá tudjad alakítani. Vagy ha kicsit belegondolsz, kis gyakorlással ránézésre látszik, hogy a számláló éppen (a-3)². De persze teljesen jó az is, ha a megoldóképletet használod.
> a kapott 2 gyök előjelét "megcserélem" úgy, hogy:
> 5a*(x-gyök1)*(x-gyök2)
Így van, de megint: nem x, hanem 'a' a változó neve. Vagyis:
5a · (a-gyök1) · (a-gyök2)
A két gyök 2 és 3, vagyis a nevező 5a(a-2)(a-3).
A tört tehát:
(a-3)² / 5a(a-2)(a-3)
Az (a-3) ott van a számlálóban és a nevezőben is, lehet vele egyszerűsíteni, vagyis ez lesz:
a-3 / 5a(a-2)
És most tadaaam
Megjegyzés:
Most már nincs a nevezőben (a-3), vagyis ez a nevező nem lesz nulla a=3 esetén. Ennek ellenére mivel az eredeti kifejezés nincs értelmezve a=3-nál, továbbra is, ezzel a törttel is az van, hogy a ∈ ℝ \ {0, 2, 3}
Ha bármi nem tiszta, kérdezz rá.
1
- Még nem érkezett komment!