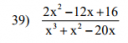Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
"Egyszerűsítse a törteket a változók lehetséges értékei mellett"
 noxter-norxert1704
kérdése
noxter-norxert1704
kérdése
1029
Először leírnék egyet, amit sikerült megoldanom, és utána leírom azt, ami már nem megy.
Jó lenne, ha át tudnám látni a dolgokat, hogy mi honnan jön.
Ami ment:
x^2 - 2x - 15 / x^2 - 4x -5 -> (x-1)^2 - 16 / (x-2)^2 - 9 -> ..... -> (x-5)(x+3) / (x-5)(x+2) = x+3 / x+2
Ami nem megy:
2x^2 - 9x +10 / 2x^2 + x - 15
Jó lenne, ha át tudnám látni a dolgokat, hogy mi honnan jön.
Ami ment:
x^2 - 2x - 15 / x^2 - 4x -5 -> (x-1)^2 - 16 / (x-2)^2 - 9 -> ..... -> (x-5)(x+3) / (x-5)(x+2) = x+3 / x+2
Ami nem megy:
2x^2 - 9x +10 / 2x^2 + x - 15
Jelenleg 1 felhasználó nézi ezt a kérdést.
tört, egyszerűsítés, azonosság
tört, egyszerűsítés, azonosság
0
Középiskola / Matematika
Válaszok
6 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Ha az zavar, hogy elől van a 2-es, akkor egyszerűsítsd a törtet 2-vel:
Számláló: x² - 4,5x + 5
Nevező: x² + 0,5x - 7,5
Egyébként pedig úgy érdemes megoldani, ahogyan a https://ehazi.hu/q/9879 kérdésednél jártunk el.
Számláló: x² - 4,5x + 5
Nevező: x² + 0,5x - 7,5
Egyébként pedig úgy érdemes megoldani, ahogyan a https://ehazi.hu/q/9879 kérdésednél jártunk el.
Módosítva: 8 éve
0
- Még nem érkezett komment!
 noxter-norxert1704
válasza
noxter-norxert1704
válasza
Esetleg azt még meg tudod mondani nekem, hogy mikor kell ezt az "oldjuk meg az egyenletet" módszert használni?
Mert nem látom át a logikáját.
Így, hogy mondod, hogyan oldjam meg, már gondolom menni fog, de nem jönnék rá magamtól.
És azt a részét sem értettem, hogy miért változtattad meg az előjelét a két eredménynek?
Akkor kell ezt használni, amikor a középső elem, azaz a sima "x" olyan érték, amit nem lehet kapni általában szimpla (a+b)^2 azonosságból?
Mert nem látom át a logikáját.
Így, hogy mondod, hogyan oldjam meg, már gondolom menni fog, de nem jönnék rá magamtól.
És azt a részét sem értettem, hogy miért változtattad meg az előjelét a két eredménynek?
Akkor kell ezt használni, amikor a középső elem, azaz a sima "x" olyan érték, amit nem lehet kapni általában szimpla (a+b)^2 azonosságból?
Módosítva: 8 éve
0
- Még nem érkezett komment!
 noxter-norxert1704
válasza
noxter-norxert1704
válasza
És még nem is említettem meg az utolsó feladatát ennek a témakörnek, pedig ennél az utolsó előttinél is már mennyire el vagyok akadva.. lelombozó
Ennek a felső részét át tudtam alakítani (x-3)^2 -1 -re, am tök jó, de hogy az alsó résszel mit csináljak, fogalmam sincs.
Kiemeltem x-et, akkor a másodfokúnak az eredménye -5 és 4 lett, de hogy ezzel a két számmal mit csináljak már fogalmam sincs.
Ha van időd és türelmed ezt is megmondani, meg segíteni megérteni, akkor örök hálám
Ennek a felső részét át tudtam alakítani (x-3)^2 -1 -re, am tök jó, de hogy az alsó résszel mit csináljak, fogalmam sincs.
Kiemeltem x-et, akkor a másodfokúnak az eredménye -5 és 4 lett, de hogy ezzel a két számmal mit csináljak már fogalmam sincs.
Ha van időd és türelmed ezt is megmondani, meg segíteni megérteni, akkor örök hálám

0
-
Rantnad: Kiemelsz a nevezőből x-et, ekkor x*(x^2+x-20)-at kapsz, aztán az x^2+x-20-at tovább bontod szorzatalakba. A végeredmény x*(x+5)*(x-4). 8 éve 1
-
Rantnad: Ja, és a számlálóban, ha már így állsz neki, 2*((x-3)^2-1) lesz. 8 éve 1
 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
Azt hittem, hogy ismered ezt a képletet, de akkor kifejtem bővebben;
első körben nézzük ezt az egyenletet: (x-1)*(x+2)=0. Ennek a megoldásait ránézésre meg tudjuk mondani; egy szorzat értéke akkor 0, hogy valamelyik tényezője 0, így vagy x-1=0, tehát x=1, vagy x+2=0, tehát x=-2.
Az egyenletet úgy is meg tudjuk oldani, hogyha kibontjuk a zárójelet: x²+x-2=0, ennek a megoldásai természetesen szintén 1 és -2. Ebből következően, hogyha meg tudjuk adni a másodfokú kifejezés gyökét/gyökeit, akkor fel tudjuk írni szorzatalakban, csupán azt kihasználva, hogy ugyanazok a gyökei. A szorzatalak tényezői "x-valami" alakúak, és természetesen úgy kell őket "beállítani", hogy pont akkor legyen az értékük 0, amikor az eredetinek is.
Nézzünk egy másik példát: x²-4x+3=0, ennek a gyökei 1 és 3. Ha azt akarjuk, hogy az egyik szorzótényező értéke 0 legyen x=1 esetén, akkor x-1-et kell választanunk, hasonló okokból x-3 lesz a másik jó választás, tehát a keresett szorzatalak: (x-1)*(x-3). Ha kibontjuk, pont az eredetit kapjuk vissza.
Másik példa: x²+6x+8=0, itt a gyökök -2 és -4. Ha azt akarjuk, hogy x=-2 esetén 0 legyen az egyik tényező, akkor x+2-t kell választanunk, a másik x+4 lesz, tehát (x+2)*(x+4) lesz a keresett alak.
Legyen még egy példa, hogy minden lehetőséget lefedjünk; 3x²+6x-9=0, ennek a gyökei 1 és -3. A fenti analógiát követve (x-1)*(x+3) lesz a keresett alak, viszont ezzel van egy kis bökkenő; ha kibontjuk, akkor x²+2x-3-at kapunk, ami nem éppen 3x²+6x-9, de szerencsére meg tudjuk javítani azzal, hogyha beszorozzuk 3-mal, tehát ebben az esetben 3*(x-1)*(x+3) lesz a szorzatalak. Az is észrevehető, hogy a 3 pont a főegyüttható (az a szám, amivel x² szorozva van).
Általánosan tehát úgy lehet leírni, hogyha adott egy másodfokú polinom, melynek főegyütthatója a, gyökei x₁ és x₂, akkor a másodfokú polinom felírható a*(x-x₁)*(x-x₂) alakban. Ha véletlenül x₁=x₂ lenne, akkor a*(x-x₁)² alakban is felírható. Ebből az is következik, hogy ha egy adott számhalmazon nincs gyöke a polinomnak, akkor nem írható fel szorzatalakban, ilyen például a klasszikus x²+1 is (komplex számkörben viszont van gyöke, ott felírható (x-i)*(x+i) alakban, de ez már felsőbb matematika).
első körben nézzük ezt az egyenletet: (x-1)*(x+2)=0. Ennek a megoldásait ránézésre meg tudjuk mondani; egy szorzat értéke akkor 0, hogy valamelyik tényezője 0, így vagy x-1=0, tehát x=1, vagy x+2=0, tehát x=-2.
Az egyenletet úgy is meg tudjuk oldani, hogyha kibontjuk a zárójelet: x²+x-2=0, ennek a megoldásai természetesen szintén 1 és -2. Ebből következően, hogyha meg tudjuk adni a másodfokú kifejezés gyökét/gyökeit, akkor fel tudjuk írni szorzatalakban, csupán azt kihasználva, hogy ugyanazok a gyökei. A szorzatalak tényezői "x-valami" alakúak, és természetesen úgy kell őket "beállítani", hogy pont akkor legyen az értékük 0, amikor az eredetinek is.
Nézzünk egy másik példát: x²-4x+3=0, ennek a gyökei 1 és 3. Ha azt akarjuk, hogy az egyik szorzótényező értéke 0 legyen x=1 esetén, akkor x-1-et kell választanunk, hasonló okokból x-3 lesz a másik jó választás, tehát a keresett szorzatalak: (x-1)*(x-3). Ha kibontjuk, pont az eredetit kapjuk vissza.
Másik példa: x²+6x+8=0, itt a gyökök -2 és -4. Ha azt akarjuk, hogy x=-2 esetén 0 legyen az egyik tényező, akkor x+2-t kell választanunk, a másik x+4 lesz, tehát (x+2)*(x+4) lesz a keresett alak.
Legyen még egy példa, hogy minden lehetőséget lefedjünk; 3x²+6x-9=0, ennek a gyökei 1 és -3. A fenti analógiát követve (x-1)*(x+3) lesz a keresett alak, viszont ezzel van egy kis bökkenő; ha kibontjuk, akkor x²+2x-3-at kapunk, ami nem éppen 3x²+6x-9, de szerencsére meg tudjuk javítani azzal, hogyha beszorozzuk 3-mal, tehát ebben az esetben 3*(x-1)*(x+3) lesz a szorzatalak. Az is észrevehető, hogy a 3 pont a főegyüttható (az a szám, amivel x² szorozva van).
Általánosan tehát úgy lehet leírni, hogyha adott egy másodfokú polinom, melynek főegyütthatója a, gyökei x₁ és x₂, akkor a másodfokú polinom felírható a*(x-x₁)*(x-x₂) alakban. Ha véletlenül x₁=x₂ lenne, akkor a*(x-x₁)² alakban is felírható. Ebből az is következik, hogy ha egy adott számhalmazon nincs gyöke a polinomnak, akkor nem írható fel szorzatalakban, ilyen például a klasszikus x²+1 is (komplex számkörben viszont van gyöke, ott felírható (x-i)*(x+i) alakban, de ez már felsőbb matematika).
Módosítva: 8 éve
0
- Még nem érkezett komment!
 noxter-norxert1704
válasza
noxter-norxert1704
válasza
Köszi 
Egyébként volt valami módszer amivel ránézésre meg lehetett az egyszerűbb másodfokúnál mondani a gyökei értékét.
Ezt már elfelejtettem, hogyan volt pontosan.
Meg tudod mondani? Hasznos lehet
Hasznos lehet 
Elég, ha az előbb leírt példáidat használod fel, pl. a legutolsót.
Én annál nem látnám ránézésre, hogy mik a gyökei.

Egyébként volt valami módszer amivel ránézésre meg lehetett az egyszerűbb másodfokúnál mondani a gyökei értékét.
Ezt már elfelejtettem, hogyan volt pontosan.
Meg tudod mondani?
 Hasznos lehet
Hasznos lehet 
Elég, ha az előbb leírt példáidat használod fel, pl. a legutolsót.

Én annál nem látnám ránézésre, hogy mik a gyökei.

0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
Meg lehet mondani ránézésre, de nem biztos, hogy érdemes, bele tud kavarodni az ember. Azért elmondom majd, de először két másik módszer:
1) Megoldóképlet
Ez az, amit Rantnad elmagyarázott. Kiszámolod a gyököket a megoldóképlettel, stb.
2) Teljes négyzetté alakítás
Ez az, amit te csináltál fent a kérdésnél. Ez is nagyon jó módszer és elég gyors is:
2x² - 12x + 16 = 2(x² - 6x + 8) = 2( (x-3)² - 1² ) = 2(x-3-1)(x-3+1) = 2(x-4)(x-2)
3) "Ránézésre"
Ez valójában a Viète formulákon alapul. Ha van egy ilyen másodfokú kifejezés:
x² + bx + c
Akkor ennek a gyökei (x₁ és x₂) között ez teljesül:
x₁+x₂ = -b
x₁·x₂ = c
Vigyázat, az x²-nek 1 volt az együtthatója a kifejezésben! Ha nem 1, kicsit más lesz a két formula, de azt most hagyjuk.
A mostani feladatban:
2x² - 12x + 16 = 2(x² - 6x + 8) = 2(x² - (x₁+x₂)x + x₁·x₂)
A gyökök szorzata tehát 8, összege pedig 6. És most találgatni kell: Ránézésre ez 2·4 és 2+4, vagyis ez lesz a szorzat:
2(x-2)(x-4)
A nevezővel:
x³ + x² - 20x = x·(x² + x - 20)
A gyökök szorzata tehát -20, összege pedig -1, ami kis találgatással -5 és 4. Tehát a szorzat:
x·(x-x₁)(x-x₂) = x·(x+5)(x-4)
... bele lehet kavarodni az előjelekbe...
1) Megoldóképlet
Ez az, amit Rantnad elmagyarázott. Kiszámolod a gyököket a megoldóképlettel, stb.
2) Teljes négyzetté alakítás
Ez az, amit te csináltál fent a kérdésnél. Ez is nagyon jó módszer és elég gyors is:
2x² - 12x + 16 = 2(x² - 6x + 8) = 2( (x-3)² - 1² ) = 2(x-3-1)(x-3+1) = 2(x-4)(x-2)
3) "Ránézésre"
Ez valójában a Viète formulákon alapul. Ha van egy ilyen másodfokú kifejezés:
x² + bx + c
Akkor ennek a gyökei (x₁ és x₂) között ez teljesül:
x₁+x₂ = -b
x₁·x₂ = c
Vigyázat, az x²-nek 1 volt az együtthatója a kifejezésben! Ha nem 1, kicsit más lesz a két formula, de azt most hagyjuk.
A mostani feladatban:
2x² - 12x + 16 = 2(x² - 6x + 8) = 2(x² - (x₁+x₂)x + x₁·x₂)
A gyökök szorzata tehát 8, összege pedig 6. És most találgatni kell: Ránézésre ez 2·4 és 2+4, vagyis ez lesz a szorzat:
2(x-2)(x-4)
A nevezővel:
x³ + x² - 20x = x·(x² + x - 20)
A gyökök szorzata tehát -20, összege pedig -1, ami kis találgatással -5 és 4. Tehát a szorzat:
x·(x-x₁)(x-x₂) = x·(x+5)(x-4)
... bele lehet kavarodni az előjelekbe...

Módosítva: 8 éve
1
- Még nem érkezett komment!