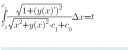Ez egy funkcionál minimalizálásával kapcsolatos probléma.
Gondolom a variációszámítás c. tárgyból szeretnéd a vizsgáidat
és a szigorlataidat letenni.

Első közelítésben itt a neten javaslom átolvasni ezeket:

https://en.wikipedia.org/wiki/Calculus_of_variations

illetve magyar nyelven olvasható dolgozat:

Variációszámítás
Szakdolgozat
Matematika alapszak
Matematikus szakirány
Szerző: Boskovits Gábor
Témavezető: Csikós Balázs

Kósa András is írt Variációszámítás c. tankönyvet, amely valamikor 40 évvel
ezelőtt jelent meg. Talán valamelyik könyvtár tudna ebben segíteni.

Az az igazság én is írtam erről egy kb. 30 oldalas dolgozatot, de mire én ehhez
újból hozzáférek, újból áttanulmányozom, újból megértem kell egy kis idő.
(Volna még egy észrevételem, azt lásd a leveleid között.)

A variációszámítás az analízisnek a (valós) funkcionálok szélsőértékének vizsgálatával foglalkozó része. A legegyszerűbb ilyen funkcionáltípus (feladattípus) a következő. Legyen `T` síkbeli tartománynak `P_1 (x_1, y_1)` és `P_2 (x_2, y_2)` két rögzített pontja, amelyekre `x_1<x_2`; legyen továbbá `f(x, y, y')` kétszer folytonosan differenciálható valós függvény, amely értelmezve van `x, y` és `y'` minden olyan értékére, amelyre `(x,y) in T` és y' tetszőleges valós szám (az f neve alapfüggvény). Értelmezzünk egy `I` funkcionált a következőképpen: (a) A I értelmezési tartományát alkossák azok az `[x_1, x_2]` intervallumban értelmezett , kétszer folytonosan differenciálható y egyváltozós valós függvények, amelyekre `graf` ` y` `sub` `T` és `y(x_1)=y_1`; `y(x_2)=y_2`. Ezeket `I` megengedett függvényeinek nevezik.
(b) Minden y megengedett függvényhez rendeljük hozzá az `I[y]=int_(x_1)^(x_2) f(x, y, y') dx` valós számot (itt `I[y]`: az I funkcionál helyettesítési értéke az y függvényen, ahol `y'` az `y` deriváltfüggvénye ) Fontos probléma: van-e olyan megengedett függvény (s ha van, melyik az), amelyre a vizsgált funkcionál minimális. A szélsőértéket adó extremális függvények meghatározására vonatkozó fontos tétel: Ha az `I` funkcionál az `y` megengedett függvényen szélsőértéket vesz fel, akkor ki kell elégítenie az `f'_y-frac{d}{dx}f'_(y')=0` ún. Euler-Lagrange-féle differenciálegyenletet, ami tömör felírási módja az
`f'_(y) (x, y, y')-f''_(xy') (x, y, y')-f''_(yy') (x, y, y')y'-f''_(y'y') (x, y, y')y''=0` másodrendű közönséges differenciálegyenletnek.

Emlékeztető. `f(x, y(x), z(x))` "háromváltozós" összetett függvény differenciálási szabálya: a belső függvény deriváltjának és a külső függvény deriváltjának a skaláris szorzata.
`frac{d}{dx}f(x, y(x), z(x))=f'_(x)(x, y(x), z(x))+f'_(y)(x, y(x), z(x))frac{dy}{dx}+f'_(z)(x, y(x), z(x))frac{dz}{dx}.`

Visszatérve a kiindulási feladatra, nyugodtan elmondhatjuk ezek után, hogy az alapfüggvényed a következő alakú lesz: `f(x, y, y')=frac{sqrt(1+(y')^2)}{sqrt(x^2+y^2)c_1+c_0}`, amelyről el kell döntened, hogy a fent leírt kikötéseknek eleget tesz-e. A felírandó E-L-féle másodrendű differenciálegyenlet egy kezdeti érték problémát takar, és amelynek megoldása lesz az általad t[y]-al jelölhető funkcionálnak. Feladatod eredete mechanika tárgykörében születhetett.
Hátra van még a differenciálegyenlet felállítása:
`frac {- (y''(x)·(c_0·sqrt(y(x)^2 + x^2) + c_1·y(x)^2 + c_1·x^2) + c_1·(y(x) - x·y'(x))·(y'(x)^2 + 1))}
{((c_1·sqrt(y(x)^2 + x^2) + c_0)^2·sqrt(y(x)^2 + x^2)·(y'(x)^2 + 1)^(3/2))}=0`

Néhány gondolatot írnék a variáció eredetéről. Ismert, hogy a funkcionál a valós függvény (illetve komplex értékeket felvevő függvény) szinonimája, ahol az értelmezési tartomány nem valamilyen számtartomány, hanem vektorok vagy függvények vagy görbék vagy felületek. Az értékkészlet lesz valamilyen számtartomány. A differenciállal kapcsolatos analóg fogalmat találunk a funkcionálok esetén is. Újra elővéve a fent definiált `I[y]` funkcionált az `y` megengedett függvényen, ahol `f` folytonosan differenciálható függvény, ekkor az funkcionálnak `y`-ra vonatkozó első variációján a `delta I_y`-al jelölt lineáris funkcionált értjük:
`delta I_y[eta]=int_(x_1)^(x_2)(f'_y(x, y(x), y'(x))*eta(x)+f'_(y')(x, y(x), y'(x))*eta'(x))dx`, ahol `f'_y` és `f'_(y')` az `f ` függvény parciális derivált függvényei, `eta` pedig tetszőleges olyan kétszer folytonosan deriválható függvény, amelyre `eta(x_1)=eta(x_2)=0`. Ha `y`-on az `I` funkcionál szélsőértéket vesz fel, akkor `delta I_y`=0 (azonosan nulla), amely (egy másik tételre hivatkozva) feltétel ekvivalens azzal, hogy az `y` függvény kielégíti az Euler-Lagrange-féle differenciálegyenletet. A mechanika variációs elvei is felhasználják ezeket a fogalmakat.