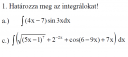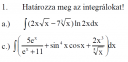Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Integrálok meghatározása
 marika15
kérdése
marika15
kérdése
539
Hiába próbálkozok sajnos nem tudom megoldani ezeket az integrálokat és hamarosan itt a vizsga. Remélem, hogy tud valaki nekem segíteni egy megoldással (esetleg rövid kis magyarázattal), hátha jobban át tudom látni a megoldási lépéseket. Na meg gyakorolni is könnyebb, ha tudom, hogy mit kell kapjak. Már annak is örülök, ha csak 1 megoldásra kerül 
Előre is köszönöm a segítséget!

Előre is köszönöm a segítséget!
Jelenleg 1 felhasználó nézi ezt a kérdést.
integrálás, integrál
integrálás, integrál
0
Felsőoktatás / Matematika
Válaszok
1 gyula205
válasza
gyula205
válasza
Legtöbb fiatal hölgynek az a szokása, hogy néhány nappal a dolgozat vagy vizsga előtt akarja megérteni, begyakorolni és megtanulni a matekot. Na ezzel az integrálszámítással ezt nem lehet megcsinálni. Oktatócsomagjaim szerte széjjel vannak, de most megpróbálok arra vállalkozni, hogy az eredményes vizsgádra legyen valamilyen sanszod is. Én egy idősebb matekos volnék, jelenleg is kutatok, de tanítok is és rendszeresen megjelenek itt az ehazi.hu-n is.
Első közelítésben megkérdezném, hogy szoktál-e matematika szoftvereket használni. Remek gyakorlási felületet ad a https://mathworld.wolfram.com/ portálon a WolframAlpha interaktív matematikai kalkulátor. A parancssora egysoros. A műveleti jelek, operátorok és függvények az Excelben megszokott szintaktikával érhetők el. Csak nem kell a parancs elé kitenni az = jelet.
Nézzük hogyan történik egy egyszerű integrál bevitele: int x^5 dx. És a program néhány másodpercben a parancssoron kívüli területre prezentálja az eredményt. Most egy interrupt-ot adok és megkérdezném, hogy vannak-e matematikával kapcsolatos egyetemi jegyzeteid, segédletek és/vagy szakkönyvek. Keresd meg, hogy ott van-e köztük Bárczy Barnabás Integrálszámítás c. szakkönyve. Mert szerintem 1970 óta ez a legjobb amit valaha itt írtak Magyarországon. Azóta megélt vagy tucatra való kiadást a Bolyai sorozatban.
Tudom nincs időd, lássuk tehát a medvét!
Ugyan 4 integrált raktál fel, de valójában 2x2 csoportban 5+6 db. függvényt kellene kiszámolni. Figyelembe véve azt a kellemes tulajdonságot, hogy lehet tagonként integrálni, ebből a 11 részfeladatból kivadászható 3 olyan ami viszonylag könnyű. Ezekből az egyik exponenciális a másik kettő hatványfüggvény (egytagú polinom).
Állapodjunk meg abban, ha írok egy megoldást, akkor nem írom ki mindig a konstanst az időmegtakarítás kedvéért.
Általános megoldóképletük: `int a^(bx+c) dx=int e^(ln(a)*(bx+c))dx=frac{e^(ln(a)*(bx+c))}{b*ln(a)}`.
A másik csoport általános megoldóképlete: `int x^b dx=frac{x^(b+1)}{(b+1)}`.
Látogass még el ide is:
https://regi.tankonyvtar.hu/hu/tartalom/tamop425/0027_MAT4/ch01s02.html
https://hu.wikipedia.org/wiki/Riemann-integr%C3%A1l%C3%A1s belül az alapintegrálok táblázatára. Én legközelebb holnap délutáni jelentkezésemmel folytatnám, ha még nem késő.
Tehát még nem késő. Teljesség igénye nélkül írom e sorokat. Amivel Te foglalkozni szeretnél azt hívják határozatlan integrálnak vagy antideriváltnak is. Felfogható egy lineáris operátornak is, mert `int (a*f(x)+b*g(x))dx=a*int f(x) dx+b*int g(x) dx` ahol `a, b in RR`. Konkrétabban foglalkozzunk tehát a három legkönnyebb esettel. A bal kép c/3 függvénye `7x` egy nagyon egyszerű polinom, amelynek együtthatója `7` és kitevője `1`. Nézz rá a fent leírt második esetre, mert oda illik. Az együtthatóval nem nagyon kell törődni, csak a kitevővel, ami itt b=1. Ebből következik, hogy `int 7*x dx= 7*frac{x^2}{2}`. A jobb kép c/3 függvénye `frac{2x^3}{root(5)(x)}`. Az együtthatóval itt sem törődünk és átalakítjuk, ahogy azt a középiskolában tanították. Tehát `frac{2x^3}{x^(1/5)}=2x^(3-frac{1}{5})=2x^frac{14}{5}`. Megint a fent leírt második eset, mert itt `b=frac{14}{5}`. Tehát az integrál eredménye `frac{2x^(frac{14}{5}+1)){frac{14}{5}+1}=frac{10x^frac{19}{5}}{19}`. A bal kép c/2 exponenciális függvénye `2^(-2x)` a fent leírt első esetének fogható fel, ahol `a=2`, `b=-2` és `c=0`. Tehát `int 2
^(-2x+0) dx=int e^(ln(2)*(-2x))dx=frac{e^(ln(2)*(-2x))}{-2*ln(2)}`.
Most visszatérnék az alapintegrálok táblázatára. Javaslom, hogy ebből a táblázatból inkább a felső négy sorban található függvényekre koncentrálj! Elvileg ha ezekből minél többet tudunk, annál jobb eséllyel alkalmazhatod a Wikipédián is leírt nevezetes alesetek valamelyikét. Az a négy eset bőven elegendőnek tűnik, szerintem a vizsgán úgy sem fogsz remekelni. Ott is érdemes a helyettesítéses integrálásra és a lineáris belső függvény esetére koncentrálni. Ez utóbbi módszerre adnak alkalmat a bal kép c/1-es `sqrt((5x-1)^7)` és c/3-es `cos(6-9x)` függvényei. Ugyanis a külső függvény egyiknél `x^(7/2)` a másiknál `cos(x)`. A megoldások motorjai ezek az un. külső függvények integráljai lesznek, majd a végén osztunk a lineáris tag együtthatójával. Tehát `int (5x-1)^(7/2) dx=frac{(5x-1)^frac{9}{2}}{frac{5*9}{2}} =frac{2(5x-1)^frac{9}{2}}{45}` valamint `int cos(6-9x) dx=frac{sin(6-9x)}{-9}=frac{sin(9x-6)}{9}`.
Helyettesítéses integrálásra ad lehetőséget a jobb kép c/1-es függvénye. Itt egyszerűbb algebrai függvényhez jutunk az `u=e^x` és `du=e^x*dx` által. Tehát `int frac{(5e^x)dx}{e^x+11}=int frac{5du}{u+11}=5ln(u+11)=5ln(e^x+11)`.
Végül a parciális integrálás technikájáról írnék egy-két gondolatot. Aki ezt hibátlanul elvégzi, annak már komolyabban kell működtetnie a szürke állományát. Ilyen a jobb kép a/1-2 feladata. Azt a bizonyos `u'` behelyettesítést a transzcendensebbnek tűnő függvényre érdemes elvégezni. Itt először egy kicsivel általánosabbnak tűnő integrállal számolnék. Legyen tehát `v(x)=ax+b` és `u'(x)=sin(cx)` valamint `v'(x)=a` és `u(x)=frac{-cos(cx)}{c}`. Tehát `int ubrace((ax+b)*sin(cx))_(" vu' ") dx=ubrace(frac{-(ax+b)cos(cx)}{c})_(" v u ")-int ubrace((frac{-cos(cx)}{c})*a)_(" uv' ")dx=frac{-(ax+b)cos(cx)}{c}+frac{a*sin(cx)}{c^2}`. `a=4` és `b=-7` és `c=3` esetben az eredmény a fentiekre hivatkozva `frac{-(4x-7)cos(3x)}{3}+frac{4*sin(3x)}{9}`.
Végül a bal kép a/1-2 feladataihoz ad segítséget a következő megoldóképlet:
`int x^b*ln(ax)dx=frac{x^(b + 1)·ln(a·x)}{b + 1} - frac{x^(b + 1)}{(b + 1)^2}`.
Első közelítésben megkérdezném, hogy szoktál-e matematika szoftvereket használni. Remek gyakorlási felületet ad a https://mathworld.wolfram.com/ portálon a WolframAlpha interaktív matematikai kalkulátor. A parancssora egysoros. A műveleti jelek, operátorok és függvények az Excelben megszokott szintaktikával érhetők el. Csak nem kell a parancs elé kitenni az = jelet.
Nézzük hogyan történik egy egyszerű integrál bevitele: int x^5 dx. És a program néhány másodpercben a parancssoron kívüli területre prezentálja az eredményt. Most egy interrupt-ot adok és megkérdezném, hogy vannak-e matematikával kapcsolatos egyetemi jegyzeteid, segédletek és/vagy szakkönyvek. Keresd meg, hogy ott van-e köztük Bárczy Barnabás Integrálszámítás c. szakkönyve. Mert szerintem 1970 óta ez a legjobb amit valaha itt írtak Magyarországon. Azóta megélt vagy tucatra való kiadást a Bolyai sorozatban.
Tudom nincs időd, lássuk tehát a medvét!
Ugyan 4 integrált raktál fel, de valójában 2x2 csoportban 5+6 db. függvényt kellene kiszámolni. Figyelembe véve azt a kellemes tulajdonságot, hogy lehet tagonként integrálni, ebből a 11 részfeladatból kivadászható 3 olyan ami viszonylag könnyű. Ezekből az egyik exponenciális a másik kettő hatványfüggvény (egytagú polinom).
Állapodjunk meg abban, ha írok egy megoldást, akkor nem írom ki mindig a konstanst az időmegtakarítás kedvéért.
Általános megoldóképletük: `int a^(bx+c) dx=int e^(ln(a)*(bx+c))dx=frac{e^(ln(a)*(bx+c))}{b*ln(a)}`.
A másik csoport általános megoldóképlete: `int x^b dx=frac{x^(b+1)}{(b+1)}`.
Látogass még el ide is:
https://regi.tankonyvtar.hu/hu/tartalom/tamop425/0027_MAT4/ch01s02.html
https://hu.wikipedia.org/wiki/Riemann-integr%C3%A1l%C3%A1s belül az alapintegrálok táblázatára. Én legközelebb holnap délutáni jelentkezésemmel folytatnám, ha még nem késő.
Tehát még nem késő. Teljesség igénye nélkül írom e sorokat. Amivel Te foglalkozni szeretnél azt hívják határozatlan integrálnak vagy antideriváltnak is. Felfogható egy lineáris operátornak is, mert `int (a*f(x)+b*g(x))dx=a*int f(x) dx+b*int g(x) dx` ahol `a, b in RR`. Konkrétabban foglalkozzunk tehát a három legkönnyebb esettel. A bal kép c/3 függvénye `7x` egy nagyon egyszerű polinom, amelynek együtthatója `7` és kitevője `1`. Nézz rá a fent leírt második esetre, mert oda illik. Az együtthatóval nem nagyon kell törődni, csak a kitevővel, ami itt b=1. Ebből következik, hogy `int 7*x dx= 7*frac{x^2}{2}`. A jobb kép c/3 függvénye `frac{2x^3}{root(5)(x)}`. Az együtthatóval itt sem törődünk és átalakítjuk, ahogy azt a középiskolában tanították. Tehát `frac{2x^3}{x^(1/5)}=2x^(3-frac{1}{5})=2x^frac{14}{5}`. Megint a fent leírt második eset, mert itt `b=frac{14}{5}`. Tehát az integrál eredménye `frac{2x^(frac{14}{5}+1)){frac{14}{5}+1}=frac{10x^frac{19}{5}}{19}`. A bal kép c/2 exponenciális függvénye `2^(-2x)` a fent leírt első esetének fogható fel, ahol `a=2`, `b=-2` és `c=0`. Tehát `int 2
^(-2x+0) dx=int e^(ln(2)*(-2x))dx=frac{e^(ln(2)*(-2x))}{-2*ln(2)}`.
Most visszatérnék az alapintegrálok táblázatára. Javaslom, hogy ebből a táblázatból inkább a felső négy sorban található függvényekre koncentrálj! Elvileg ha ezekből minél többet tudunk, annál jobb eséllyel alkalmazhatod a Wikipédián is leírt nevezetes alesetek valamelyikét. Az a négy eset bőven elegendőnek tűnik, szerintem a vizsgán úgy sem fogsz remekelni. Ott is érdemes a helyettesítéses integrálásra és a lineáris belső függvény esetére koncentrálni. Ez utóbbi módszerre adnak alkalmat a bal kép c/1-es `sqrt((5x-1)^7)` és c/3-es `cos(6-9x)` függvényei. Ugyanis a külső függvény egyiknél `x^(7/2)` a másiknál `cos(x)`. A megoldások motorjai ezek az un. külső függvények integráljai lesznek, majd a végén osztunk a lineáris tag együtthatójával. Tehát `int (5x-1)^(7/2) dx=frac{(5x-1)^frac{9}{2}}{frac{5*9}{2}} =frac{2(5x-1)^frac{9}{2}}{45}` valamint `int cos(6-9x) dx=frac{sin(6-9x)}{-9}=frac{sin(9x-6)}{9}`.
Helyettesítéses integrálásra ad lehetőséget a jobb kép c/1-es függvénye. Itt egyszerűbb algebrai függvényhez jutunk az `u=e^x` és `du=e^x*dx` által. Tehát `int frac{(5e^x)dx}{e^x+11}=int frac{5du}{u+11}=5ln(u+11)=5ln(e^x+11)`.
Végül a parciális integrálás technikájáról írnék egy-két gondolatot. Aki ezt hibátlanul elvégzi, annak már komolyabban kell működtetnie a szürke állományát. Ilyen a jobb kép a/1-2 feladata. Azt a bizonyos `u'` behelyettesítést a transzcendensebbnek tűnő függvényre érdemes elvégezni. Itt először egy kicsivel általánosabbnak tűnő integrállal számolnék. Legyen tehát `v(x)=ax+b` és `u'(x)=sin(cx)` valamint `v'(x)=a` és `u(x)=frac{-cos(cx)}{c}`. Tehát `int ubrace((ax+b)*sin(cx))_(" vu' ") dx=ubrace(frac{-(ax+b)cos(cx)}{c})_(" v u ")-int ubrace((frac{-cos(cx)}{c})*a)_(" uv' ")dx=frac{-(ax+b)cos(cx)}{c}+frac{a*sin(cx)}{c^2}`. `a=4` és `b=-7` és `c=3` esetben az eredmény a fentiekre hivatkozva `frac{-(4x-7)cos(3x)}{3}+frac{4*sin(3x)}{9}`.
Végül a bal kép a/1-2 feladataihoz ad segítséget a következő megoldóképlet:
`int x^b*ln(ax)dx=frac{x^(b + 1)·ln(a·x)}{b + 1} - frac{x^(b + 1)}{(b + 1)^2}`.
Módosítva: 4 éve
0
- Még nem érkezett komment!