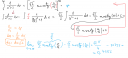Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Improprius integrál
iLoveN2O
kérdése
269
Addig meg van, hogy konvergens, de utána integrálásnál valamit elrontok... Valaki tudna egy levezetéssel szolgálni?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
2
rolandstefan
{ Vegyész }
válasza
Szia!
Esetleg kérdésed van, nyugodtan írj!
-S.R.
Esetleg kérdésed van, nyugodtan írj!
-S.R.
1
- Még nem érkezett komment!
gyula205
megoldása
A konvergencia tényét az improprius integrálokra vonatkozó majoráns kritérium
segítségével állapítjuk meg. Tudjuk, hogy ha `x gt 2`, akkor`frac{1}{2+x^2} lt frac{1}{x^2}`
Ha ezt integráljuk az adott tartományon akkor kapjuk, hogy
`lim_(xi->oo) int_2^(xi)frac{dx}{x^2}=lim_(xi->oo) [-frac{1}{x}]_2^(xi)=-0+frac{1}{2}`.
Mivel ez véges, ezért megállapítjuk a konvergencia tényét.
Visszatérve a feladatra kapjuk, hogy
`lim_(xi->oo) int_2^(xi)frac{dx}{2+x^2}=lim_(xi->oo)[frac{sqrt(2)arctg(frac{x}{sqrt(2)})}{2}]_2^(xi)=frac{sqrt(2)arctg(frac{sqrt(2)}{2})}{2} approx 0,4352... lt frac{1}{2}`.
Megjegyzés: Mivel a konvergencia tényét már Te is megcsináltad és Rolandstefan nick már megelőzött, én elfogadom megoldásnak a munkáját.
segítségével állapítjuk meg. Tudjuk, hogy ha `x gt 2`, akkor`frac{1}{2+x^2} lt frac{1}{x^2}`
Ha ezt integráljuk az adott tartományon akkor kapjuk, hogy
`lim_(xi->oo) int_2^(xi)frac{dx}{x^2}=lim_(xi->oo) [-frac{1}{x}]_2^(xi)=-0+frac{1}{2}`.
Mivel ez véges, ezért megállapítjuk a konvergencia tényét.
Visszatérve a feladatra kapjuk, hogy
`lim_(xi->oo) int_2^(xi)frac{dx}{2+x^2}=lim_(xi->oo)[frac{sqrt(2)arctg(frac{x}{sqrt(2)})}{2}]_2^(xi)=frac{sqrt(2)arctg(frac{sqrt(2)}{2})}{2} approx 0,4352... lt frac{1}{2}`.
Megjegyzés: Mivel a konvergencia tényét már Te is megcsináltad és Rolandstefan nick már megelőzött, én elfogadom megoldásnak a munkáját.
Módosítva: 2 éve
1
- Még nem érkezett komment!