Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika
 PimpXxX
kérdése
PimpXxX
kérdése
368
ábrázold és jellemezd a az f(x)=cosx+1 és a g(x)=sin(x+pi/4) fgv-eket!
Jelenleg 1 felhasználó nézi ezt a kérdést.
matek, függvény
matek, függvény
0
Középiskola / Matematika
Válaszok
1 kazah
megoldása
kazah
megoldása
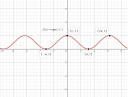
f(x) = cos(x) + 1
Függvénytranszformációk:
1. y = cos(x) alapfüggvény
2. y = cos(x) + 1 eltolás az y tengely mentén pozitív irányba 1 egységgel
jellemzés:
`k in ZZ`
ÉT: `x in RR`
ÉK: `f(x) in RR | f(x) in [0;2]`
Menete: szigorúan monoton növekvő: [`-pi+2kpi;2kpi`]
szigorúan monoton csökkenő: [`2kpi;pi+2kpi`]
Zérushely: `pi+2kpi`
korlátosság: alulról korlátos: K=0; felülről korlátos: K=2
Szélsőérték: minimum: `(-pi+2kpi;0)`
maximum: `(2kpi;2)`
paritás: páros
periodicitás: periodikus, periódusa `2pi`
folytonos.
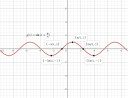
g(x) = `sin(x+pi/4)`
függvénytranszformációk:
y = sin(x) alapfüggvény
y = `sin(x+pi/4)` eltolás az x tengely mentén negatív irányba `pi/4` egységgel.
jellemzés:
`k in ZZ`
ÉT: `x in RR`
ÉK: `g(x) in RR|g(x) in [-1;1]`
menete: szigorúan monoton növekvő: [`(-3pi)/4+2kpi;pi/4+2kpi`]
szigorúan monoton csökkenő: [`pi/4+2kpi;(5pi)/4+2kpi`]
zérushely: `-pi/4+k*pi`
korlátosság: alulról korlátos: K=-1; felülről korlátos: K=1
szélsőérték: minimum: `((-3pi)/4+2kpi;-1)`; maximum: `(pi/4+2kpi;0)`
paritás: nincs
periodicitás: periódikus, periódusa `2pi`
folytonos.
Függvénytranszformációk:
1. y = cos(x) alapfüggvény
2. y = cos(x) + 1 eltolás az y tengely mentén pozitív irányba 1 egységgel
jellemzés:
`k in ZZ`
ÉT: `x in RR`
ÉK: `f(x) in RR | f(x) in [0;2]`
Menete: szigorúan monoton növekvő: [`-pi+2kpi;2kpi`]
szigorúan monoton csökkenő: [`2kpi;pi+2kpi`]
Zérushely: `pi+2kpi`
korlátosság: alulról korlátos: K=0; felülről korlátos: K=2
Szélsőérték: minimum: `(-pi+2kpi;0)`
maximum: `(2kpi;2)`
paritás: páros
periodicitás: periodikus, periódusa `2pi`
folytonos.
g(x) = `sin(x+pi/4)`
függvénytranszformációk:
y = sin(x) alapfüggvény
y = `sin(x+pi/4)` eltolás az x tengely mentén negatív irányba `pi/4` egységgel.
jellemzés:
`k in ZZ`
ÉT: `x in RR`
ÉK: `g(x) in RR|g(x) in [-1;1]`
menete: szigorúan monoton növekvő: [`(-3pi)/4+2kpi;pi/4+2kpi`]
szigorúan monoton csökkenő: [`pi/4+2kpi;(5pi)/4+2kpi`]
zérushely: `-pi/4+k*pi`
korlátosság: alulról korlátos: K=-1; felülről korlátos: K=1
szélsőérték: minimum: `((-3pi)/4+2kpi;-1)`; maximum: `(pi/4+2kpi;0)`
paritás: nincs
periodicitás: periódikus, periódusa `2pi`
folytonos.
0
- Még nem érkezett komment!