Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Beadandó SOS
Jankó
kérdése
725
Egy szimmetrikus trapéz területe 144 m2, az alapjai 15 m és 8 m hosszúak. Mekkorák a szögei és átlójának hossza?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2
velo.gabor
{ Elismert }
válasza
Szia!
A trapéz területének képlete: T=(a+c)*m/2, ahol a és c a két alap, m pedig a trapéz magassága. Tehát ebből a képletből kiszámítható a magasság ha átrendezzük: m=2T/(a+c)=2*144/(15+8)=288/23= 12,52m
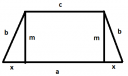
Mellékeltem egy ábrát, amin két darab derékszögű háromszög van. Ezeknek az alapját x-szel jelötem. Számoljuk ki ezt előbb:
a=c+2x /-c
a-c=2x /:2
(a-c)/2=x
(15-8)/2=x
3,5m=x
Mostmár ki tudjuk számolni a hosszabb alapon fekvő szögeket:
tgα=m/x
tgα=12,52/3,5
tgα=3,58, amiből α=74,4⁰ a másik alapon fekvő szög: β=180⁰-74,4⁰=105,6⁰
Ha berajzolóaz átlót szintén kapsz egy derékszögű háromszöget, melynek oldalai: a-x, m , e(átló). Tehát pitagorasz tétellel kiszámítható az átló:
(a-x)2+m2=e2
11,52+12,522=e2
132,25+156,75=e2
289=e2 /√
17m=e
A trapéz területének képlete: T=(a+c)*m/2, ahol a és c a két alap, m pedig a trapéz magassága. Tehát ebből a képletből kiszámítható a magasság ha átrendezzük: m=2T/(a+c)=2*144/(15+8)=288/23= 12,52m
Mellékeltem egy ábrát, amin két darab derékszögű háromszög van. Ezeknek az alapját x-szel jelötem. Számoljuk ki ezt előbb:
a=c+2x /-c
a-c=2x /:2
(a-c)/2=x
(15-8)/2=x
3,5m=x
Mostmár ki tudjuk számolni a hosszabb alapon fekvő szögeket:
tgα=m/x
tgα=12,52/3,5
tgα=3,58, amiből α=74,4⁰ a másik alapon fekvő szög: β=180⁰-74,4⁰=105,6⁰
Ha berajzolóaz átlót szintén kapsz egy derékszögű háromszöget, melynek oldalai: a-x, m , e(átló). Tehát pitagorasz tétellel kiszámítható az átló:
(a-x)2+m2=e2
11,52+12,522=e2
132,25+156,75=e2
289=e2 /√
17m=e
1
-
Jankó: Köszönöm szépen,nagyon érthető és igényes válasz. Bár a tanárom magyarázná így
5 éve
0
