Matematika házi

4)
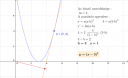
Ha az y tengely lenne a tengelye, akkor y=ax² alakú lenne az egyenlete. Ezzel párhuzamos, vagyis el van tolva vízszintesen b-vel, vagyis ez az egyenlet alakja:
y = a(x-b)²

Átmegy az (5; 4) ponton, vagyis:
4 = a(5-b)²

Az érintő meredekségét deriválással lehet megtudni... remélem, tanultátok: (majd a végén kiszámolom deriválás nélkül is... ha nem tanultatok deriválni, menj tovább)
y' = 2a·(x-b)
x=5-nél a meredekség m = 2a·(5-b)

A (4; -1) vektorra merőleges az érintő, vagyis (1; 4) az irányvektora. Ennek a meredeksége m=4/1

m = 2a(5-b) = 4

Vagyis ez a két egyenletünk van:
a(5-b) = 2
a(5-b)² = 4
Osszuk el az alsót a felsővel:
5-b = 2
b = 3
a(5-3)=2 → a = 1

Tehát az egyenlet:
y = (x-3)²

----------
Deriválás nélkül:

Az eleje ugyanaz, tehát:
y = a(x-b)²
4 = a(5-b)²

Az érintő egyenlete, ha átmegy az (5;4) ponton és normálvektora (4;-1):
4x - y = 4·5 - 4
y = 4x - 16

Ennek az egyenesnek egy közös pontja van az y = a(x-b)² egyenletű parabolával:
4x-16 = a(x-b)²
4x - 16 = ax² - 2abx + ab²
ax² - (2ab+4)x + (ab²+16) = 0
Ennek a diszkriminánsának kell 0-nak lennie, hogy csak 1 megoldás legyen:
(2ab+4)² - 4a(ab²+16) = 0
4a²b² + 16ab + 16 - 4a²b² - 64a = 0
ab + 1 - 4a = 0
a(b-4) = -1
a = 1/(4-b)
A másik egyenlet az volt, hogy 4 = a(5-b)²
4 = 1/(4-b) · (5-b)²
4(4-b) = (5-b)²
16-4b = 25-10b+b²
b² - 6b + 9 = 0
(b-3)² = 0
b = 3

a = 1/(4-3)
a = 1

Ugyanaz jött ki.

Látod amit bongolo számolt?

5)
A keresett egyenes meredeksége legyen m.
Ha jobbra megyünk 1-et, akkor m-et megy felfelé.
Ha jobbra megyünk d darabot, akkor d·m-et megy felfelé, és eljut az f egyeneshez.

(Megjegyzés: lehet, hogy d negatív, tehát balra kell menni, és az is lehet, hogy m negatív, vagyis lefelé megy akkor, amikor jobbra megy, vagy ezek bármilyen kombinációja is lehet. Majd kijön a végén. Szóval most még nem tudjuk, hogy d és m pozitív vagy negatív. A lényeg az, hogyha d-t megyünk vízszintesen és d·m-et függőlegesen, akkor pont az f egyeneshez jutunk.)

Mivel f-hez közeli harmadolópont a P, ezért az ellenkező irányba menve kétszer annyit éppen az e egyeneshez jutunk. Vagyis -2d vízszintesen és -2dm függőlegesen.

Ezekbe a pontokba jutunk P(4;1)-ből:
F(4+d; 1+dm)
E(4-2d; 1-2dm)

Az F pont az f egyenesen van, tehát behelyettesítve az F pontot f egyenletébe azonosságot kapunk:
f: x+2y=11
→ (4+d)+2(1+dm) = 11
Hasonlóan az E pont rajta van az e egyenesen:
e: x-y=-1
→ (4-2d) - (1-2dm) = -1

Meg kell oldani a fenti két egyenletből álló egyenletrendszert:
4 + d + 2 + 2dm = 11        →      d(1+2m) = 5
4 - 2d - 1 + 2dm = -1         →      d(-2+2m) = -4
----
d = 5/(1+2m)
----
5/(1+2m) · (-2+2m) = -4
5(-2+2m) = -4(1+2m)
-10 + 10m = -4 - 8m
18m = 6
m = 1/3

A P(4;1) ponton átmenő, 1/3 meredekségű egyenes egyenlete:
Az 1/3 meredekségű irányvektor (1; 1/3) vagy szebb számokkal a háromszorosa, (3; 1)
Az erre merőleges normálvektor (1; -3)
Az egyenes:
1·x - 3·y = 1·4 - 3·1
x - 3y = 1