Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
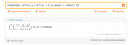
Integrálás
 Tinaa
kérdése
Tinaa
kérdése
419
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
A megadott segítséggel a feladat már nem nehéz, ugyanis az új koordinátarendszerben az integrálási tartomány egy egyszerű, a tengelyekre illeszkedő négyzetes tartomány lesz: `R_{u,v}={(u, v): -1 le u le 1 \text{ és } -1 le v le 1}`
Az integrandus az új változókkal: `(v^2)/(u+2)^2`
A régi változók kifejezése az újakkal: `x=(u+v)/2` és `y=(u-v)/2`
Innen a Jacobi-determináns: `J=|[(partial x)/(partial u),(partial x)/(partial v)],[(partial y)/(partial u),(partial y)/(partial v)]|=``|[1/2,1/2],[1/2,-1/2]|=``-1/4-1/4=-1/2`
Ennek az abszolút értékével skálázódik a tartomány mértéke a változótranszformáció hatására, vagyis `dxdy=1/2dudv`.
Most már mindent tudunk az integrál kiszámításához:
`int int_R (x-y)^2/(x+y+2)^2 dxdy=``int_{-1}^1 int_{-1}^1 (v^2)/(u+2)^2 1/2 dudv=``1/2 int_{-1}^1 1/(u+2)^2 du int_{-1}^1 v^2 dv=``1/2*[-1/(u+2)]_{-1}^1*[v^3/3]_{-1}^1=``1/2*[-1/3+1]*[1/3+1/3]=``2/9`
Egyébként az eredeti változókkal a tartomány `R={(x,y): -1 le x le 1 \text{ és } |x|-1 le y le -|x|+1}` módon paraméterezhető, ezzel numerikusan ellenőrizhető az eredmény. Mellékeltem a WolframAlpha kimenetéről képet, neki is kijött a `2/9`.
Az integrandus az új változókkal: `(v^2)/(u+2)^2`
A régi változók kifejezése az újakkal: `x=(u+v)/2` és `y=(u-v)/2`
Innen a Jacobi-determináns: `J=|[(partial x)/(partial u),(partial x)/(partial v)],[(partial y)/(partial u),(partial y)/(partial v)]|=``|[1/2,1/2],[1/2,-1/2]|=``-1/4-1/4=-1/2`
Ennek az abszolút értékével skálázódik a tartomány mértéke a változótranszformáció hatására, vagyis `dxdy=1/2dudv`.
Most már mindent tudunk az integrál kiszámításához:
`int int_R (x-y)^2/(x+y+2)^2 dxdy=``int_{-1}^1 int_{-1}^1 (v^2)/(u+2)^2 1/2 dudv=``1/2 int_{-1}^1 1/(u+2)^2 du int_{-1}^1 v^2 dv=``1/2*[-1/(u+2)]_{-1}^1*[v^3/3]_{-1}^1=``1/2*[-1/3+1]*[1/3+1/3]=``2/9`
Egyébként az eredeti változókkal a tartomány `R={(x,y): -1 le x le 1 \text{ és } |x|-1 le y le -|x|+1}` módon paraméterezhető, ezzel numerikusan ellenőrizhető az eredmény. Mellékeltem a WolframAlpha kimenetéről képet, neki is kijött a `2/9`.
Módosítva: 4 éve
0
-
Tinaa: Köszönöm szépen! 4 éve 0