Ez a csillapított harmonikus oszcillátor problémája. A testre hat a `-kx` rugóerő, valamint a `-alphav=-alpha dot x` közegellenállás. Ezek összege Newton II. törvénye szerint egyenlő az `ma=m ddot x` mennyiséggel. Tehát a mozgást leíró differenciálegyenlet a következő:

`-kx-alpha dot x = m ddot x`

Avagy szokásos alakjában:

`ddot x + alpha/m dot x + k/m x=0`

A karakterisztikus egyenlet:

`lambda^2+alpha/m lambda +k/m=0`

A sajátértékek a másodfokú egyenlet megoldóképlete alapján:

`lambda_{1,2}=-alpha/(2m) pm sqrt((alpha/(2m))^2-k/m)`

Vezessük be az `omega_0=sqrt(k/m)` sajátfrekvenciát és a `zeta=alpha/(2sqrt(mk))` csillapítást. Ezzel a sajátértékek így írhatók:

`lambda_{1,2}=omega_0 (-zeta pm sqrt(zeta^2-1))`

A differenciálegyenlet általános megoldása a következő:

`x(t)=C_1 e^{lambda_1 t}+C_2 e^{lambda_2 t}`

A `C_1` és `C_2` konstansokat a kezdeti feltételek (kezdeti kitérés és sebesség) határozzák meg. Az `x(t)` függvény alakja szempontjából három lényeges esetet kell megkülönböztetnünk:

Ha `zeta gt 1`, akkor mindkét sajátérték valós. Ilyenkor `x(t)` két valós kitevőjű exponenciális függvény összege, tehát ilyenkor nem alakul ki lengés. Ezt nevezzük túlcsillapított esetnek.

Ha `zeta=1`, akkor a két sajátérték azonos valós szám. Ilyenkor a fizikai kép hasonló, de matematikai különbség van (rezonancia lép fel a diffegyenletben), `x(t)=(C_1+tC_2)e^(- omega_0 zeta t)` alakú lesz az időfüggvény, tehát ilyenkor sem alakul ki lengés. Ezt nevezzük kritikus csillapításnak.

Ha `zeta lt 1`, akkor a sajátértékek komplex konjugált párok: `lambda_{1,2}=-omega_0 zeta pm i omega_0 sqrt(1-zeta^2)`. Ezt nevezzük alulcsillapított esetnek, ilyenkor a képzetes kitevőjű exponenciálisok trigonometrikus függvényekké vonhatók össze, és az időfüggvény alakja az alábbi lesz:

`x(t)=C e^{-omega_0 zeta t} sin(omega_0 sqrt(1- zeta^2) t + varphi)`

A `C` kezdőamplitúdót és a `varphi` kezdőfázist a kezdeti feltételek határozzák meg.

A feladat egyértelműen ez utóbbi, alulcsillapított esetről szól, hiszen a többi esetben nincs semmilyen lengés. Az időfüggvény tehát egy exponenciálisan csökkenő amplitúdójú szinusz. Nézzük meg, hogy az amplitúdó mennyi idő alatt csökken a tizedére:

`C e^{- omega_0 zeta t}=0.1C`

`omega_0 zeta t=ln 10`

`t=(ln 10)/(omega_0 zeta)`

A lengés körfrekvenciája `omega=omega_0 sqrt(1-zeta^2)`, periódusideje `T=(2pi)/omega=``(2pi)/(omega_0 sqrt(1-zeta^2))`. Oldjuk meg általánosan a feladatot, azaz határozzuk meg `T`-t, ha tudjuk, hogy az amplitúdó `N*T` idő alatt csökken a tizedére:

`NT=(ln 10)/(omega_0 zeta)`

`(2pi N)/(omega_0 sqrt(1-zeta^2))=(ln 10)/(omega_0 zeta)`

`(4pi^2 N^2)/(ln^2 10)=(1-zeta^2)/(zeta^2)`

`1/(zeta^2)=(4pi^2 N^2)/(ln^2 10)+1`

`zeta^2=(ln^2 10)/(4pi^2 N^2+ln^2 10)`

Helyettesítsük be `T` kifejezésébe ezt, valamint azt is, hogy `omega_0=``sqrt(k/m)=``sqrt(20/10)=``sqrt(2) \ \text{rad}/\text{s}`:

`T(N)=(2pi)/(sqrt(2)* sqrt(1-(ln^2 10)/(4pi^2 N^2+ln^2 10)))=``(sqrt(2)pi)/(sqrt((4pi^2 N^2)/(4pi^2 N^2+ln^2 10)))=``sqrt(2pi^2(4pi^2 N^2+ln^2 10)/(4pi^2 N^2))=``sqrt(2pi^2+(ln^2 10)/(2 N^2))`

Ennyi lesz a periódusidő másodpercben, `N` függvényében. Behelyettesítve `N` helyére a feladatban kérdezett lengésszámokat:

`T(N=4)~~4.4615\ \text{s}`
`T(N=2)~~4.5169\ \text{s}`
`T(N=3)~~4.4759\ \text{s}`
`T(N=5)~~4.4548\ \text{s}`

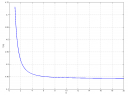
A 3. kérdéshez mellékeltem ábrát a `T(N)` függvényről. A görbe ellaposodó jellegű, az `omega_0` sajátfrekvenciához tartozó periódusidőhöz tart. Ez fizikailag is szemléletes, mivel ha nagyon sok periódus alatt csökken tizedére az amplitúdó, az azt jelenti, hogy alig-alig csillapodik a lengés, márpedig csillapítatlanul lengeni `omega_0` frekvenciával tud a rendszer.