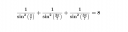Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Trigonometrikus azonosság
 szzs
{ Fortélyos } kérdése
szzs
{ Fortélyos } kérdése
722
Hogyan lehetne ezt igazolni?
Jelenleg 1 felhasználó nézi ezt a kérdést.
1
Középiskola / Matematika
Válaszok
3 Rantnad
{
Rantnad
{  }
válasza
}
válasza
Addíciós képletekkel?
0
-
szzs: Ahogy tetszik... 8 éve 0
-
szzs: ... csak valahogy segíts! 8 éve 0
 kazah
megoldása
kazah
megoldása
Valamit sikerült kihoznom, az eredményt is, vannak hézagok a hiányos matematikai ismereteim miatt.
A kiindulás:
`sin((3pi)/7)` =`sin((4pi)/7)`
illetve `sin^2(pi/7)` =a-val helyettesítek.
Nézzük a bal oldalt (és még négyzetre is emeltem, hogy haladjon):
`sin^2((3pi)/7)` = `(3*sin(pi/7)-4*sin^3(pi/7))^2` = `9*a-24*a^2+16*a^3`.
A jobb oldal kicsit hosszabb lesz, kétszer vesszük a kétszeres szögek szinuszát:
`sin^2((4pi)/7)` = `(2*sin((2pi)/7)*cos((2pi)/7))^2` = `(4*sin(pi/7)*cos(pi/7)*(1-2*sin^2(pi/7))^2` = `16*a*(1-a)*(1-2*a)^2`=`(16*a-16*a^2)*(1-4*a+4*a^2)` = `-64*a^4+128*a^3-80*a^2+16*a`.
Na ez a két kifejezés egyenlő. Összevonások után:
`64*a^4-112*a^3+56*a^2-7*a=0`
Ha az a=0-t most kihagyjuk, harmadfokú lesz az egyenlet:
`64*a^3-112*a^2+56*a-7=0`
Amit külső segítséggel megoldva:
`a_1` = `sin^2((pi)/7)`
`a_2` = `sin^2((2pi)/7)`
`a_3` = `sin^2((3pi)/7)`
Hogy miért, azt nem tudom, de leellenőriztem és annyi.
A harmadfokú egyenlet gyökei és együtthatói közötti összefüggéseket is segítségül hívva:
`a_1*a_2*a_3` = `-d/a`
`a_1*a_2+a_1*a_3+a_2*a_3` = `c/a`
`1/a_1` + `1/a_2` + `1/a_3` = `(a_1*a_2+a_1*a_3+a_2*a_3)/(a_1*a_2*a_3)` = `(c/a)/(-d/a)` = `-c/d` = `(-56)/-7` = 8
A hézagokat betömendő feladat magasabb matematikai ismeretekkel rendelkezőknek.
Köszi!
A kiindulás:
`sin((3pi)/7)` =`sin((4pi)/7)`
illetve `sin^2(pi/7)` =a-val helyettesítek.
Nézzük a bal oldalt (és még négyzetre is emeltem, hogy haladjon):
`sin^2((3pi)/7)` = `(3*sin(pi/7)-4*sin^3(pi/7))^2` = `9*a-24*a^2+16*a^3`.
A jobb oldal kicsit hosszabb lesz, kétszer vesszük a kétszeres szögek szinuszát:
`sin^2((4pi)/7)` = `(2*sin((2pi)/7)*cos((2pi)/7))^2` = `(4*sin(pi/7)*cos(pi/7)*(1-2*sin^2(pi/7))^2` = `16*a*(1-a)*(1-2*a)^2`=`(16*a-16*a^2)*(1-4*a+4*a^2)` = `-64*a^4+128*a^3-80*a^2+16*a`.
Na ez a két kifejezés egyenlő. Összevonások után:
`64*a^4-112*a^3+56*a^2-7*a=0`
Ha az a=0-t most kihagyjuk, harmadfokú lesz az egyenlet:
`64*a^3-112*a^2+56*a-7=0`
Amit külső segítséggel megoldva:
`a_1` = `sin^2((pi)/7)`
`a_2` = `sin^2((2pi)/7)`
`a_3` = `sin^2((3pi)/7)`
Hogy miért, azt nem tudom, de leellenőriztem és annyi.
A harmadfokú egyenlet gyökei és együtthatói közötti összefüggéseket is segítségül hívva:
`a_1*a_2*a_3` = `-d/a`
`a_1*a_2+a_1*a_3+a_2*a_3` = `c/a`
`1/a_1` + `1/a_2` + `1/a_3` = `(a_1*a_2+a_1*a_3+a_2*a_3)/(a_1*a_2*a_3)` = `(c/a)/(-d/a)` = `-c/d` = `(-56)/-7` = 8
A hézagokat betömendő feladat magasabb matematikai ismeretekkel rendelkezőknek.
Köszi!
0
- Még nem érkezett komment!
 bongolo
{
bongolo
{  }
válasza
}
válasza
Kazah: Nagyon szép megoldás. A kérdésedre, hogy miért pont azok az egyenlet gyökei, ez a válasz:
A kiinduló egyenleted ez:
`sin(3x)=sin(4x)`
Ennek két megoldása van:
a) `3x=4x + 2kπ`
b) `3x=π-4x + 2kπ`
a)-ból az `x_1 = 0 + 2kπ` megoldás jön, b)-ből viszont (`7x = π+2kπ`) több is:
`k=7n+0:\ x_2=π/7+2nπ`
`k=7n+1:\ x_3=(3π)/7+2nπ`
`k=7n+2:\ x_4=(5π)/7+2nπ`
`k=7n+3:\ x_5=π+2nπ`
`k=7n+4:\ x_6=(9π)/7+2nπ`
`k=7n+5:\ x_7=(11π)/7+2nπ`
`k=7n+6:\ x_8=(13π)/7+2nπ`
Viszont nem a szögek az izgalmasak, csak a szinuszuk, sőt, annak a négyzete:
`sin^2x_1=0`
`sin^2x_2=sin^2(π/7)`
`sin^2x_3=sin^2((3π)/7)`
`sin^2x_4=sin^2((5π)/7)=sin^2((2π)/7)`
`sin^2x_5=0`
`sin^2x_6=sin^2((9π)/7)=sin^2((2π)/7)`
`sin^2x_7=sin^2((11π)/7)=sin^2((3π)/7)`
`sin^2x_8=sin^2((13π)/7)=sin^2(π/7)`
Vagyis tényleg ez a 4 megoldás jön ki `a`-ra:
`a_1=0`
`a_2=sin^2(π/7)`
`a_3=sin^2((2π)/7)`
`a_4=sin^2((3π)/7)`
Viszont a teljességhez hozzátartozik, hogy nem is a fenti egyenletet oldottad meg, hanem a négyzetét:
`sin^2(3x)=sin^2(4x)`
aminek további megoldásai is vannak, hisz a két szinusz lehet ellentétes előjelű. A fentieken túl még ezek is megoldások:
c) `3x=4x+π + 2kπ`
d) `3x=-4x + 2kπ`
c)-ből a fenti `x_5` jön ki, d)-ből (`7x = 2kπ`) pedig:
`k=7n+0:\ x_9=2nπ → a_1`
`k=7n+1:\ x_(10)=(2π)/7+2nπ → a_3`
`k=7n+2:\ x_(11)=(4π)/7+2nπ → a_4`
`k=7n+3:\ x_(12)=(6π)/7+2nπ → a_2`
`k=7n+4:\ x_(13)=(8π)/7+2nπ → a_2`
`k=7n+5:\ x_(14)=(10π)/7+2nπ → a_4`
`k=7n+6:\ x_(15)=(12π)/7+2nπ → a_3`
Ezen megoldások szinuszainak a négyzete viszont nem hoz be új gyököt, odaírtam, hogy melyik `a_x`-szel azonosak.
A kiinduló egyenleted ez:
`sin(3x)=sin(4x)`
Ennek két megoldása van:
a) `3x=4x + 2kπ`
b) `3x=π-4x + 2kπ`
a)-ból az `x_1 = 0 + 2kπ` megoldás jön, b)-ből viszont (`7x = π+2kπ`) több is:
`k=7n+0:\ x_2=π/7+2nπ`
`k=7n+1:\ x_3=(3π)/7+2nπ`
`k=7n+2:\ x_4=(5π)/7+2nπ`
`k=7n+3:\ x_5=π+2nπ`
`k=7n+4:\ x_6=(9π)/7+2nπ`
`k=7n+5:\ x_7=(11π)/7+2nπ`
`k=7n+6:\ x_8=(13π)/7+2nπ`
Viszont nem a szögek az izgalmasak, csak a szinuszuk, sőt, annak a négyzete:
`sin^2x_1=0`
`sin^2x_2=sin^2(π/7)`
`sin^2x_3=sin^2((3π)/7)`
`sin^2x_4=sin^2((5π)/7)=sin^2((2π)/7)`
`sin^2x_5=0`
`sin^2x_6=sin^2((9π)/7)=sin^2((2π)/7)`
`sin^2x_7=sin^2((11π)/7)=sin^2((3π)/7)`
`sin^2x_8=sin^2((13π)/7)=sin^2(π/7)`
Vagyis tényleg ez a 4 megoldás jön ki `a`-ra:
`a_1=0`
`a_2=sin^2(π/7)`
`a_3=sin^2((2π)/7)`
`a_4=sin^2((3π)/7)`
Viszont a teljességhez hozzátartozik, hogy nem is a fenti egyenletet oldottad meg, hanem a négyzetét:
`sin^2(3x)=sin^2(4x)`
aminek további megoldásai is vannak, hisz a két szinusz lehet ellentétes előjelű. A fentieken túl még ezek is megoldások:
c) `3x=4x+π + 2kπ`
d) `3x=-4x + 2kπ`
c)-ből a fenti `x_5` jön ki, d)-ből (`7x = 2kπ`) pedig:
`k=7n+0:\ x_9=2nπ → a_1`
`k=7n+1:\ x_(10)=(2π)/7+2nπ → a_3`
`k=7n+2:\ x_(11)=(4π)/7+2nπ → a_4`
`k=7n+3:\ x_(12)=(6π)/7+2nπ → a_2`
`k=7n+4:\ x_(13)=(8π)/7+2nπ → a_2`
`k=7n+5:\ x_(14)=(10π)/7+2nπ → a_4`
`k=7n+6:\ x_(15)=(12π)/7+2nπ → a_3`
Ezen megoldások szinuszainak a négyzete viszont nem hoz be új gyököt, odaírtam, hogy melyik `a_x`-szel azonosak.
Módosítva: 7 éve
0
- Még nem érkezett komment!