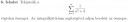SZTE matematika 1

Érdekes feladat. Az integrálkritérium csak annyit állít, hogy a `sum_{n=1}^{oo} 1/(n^2+3)` sor és az `int_1^{oo} 1/(x^2+3) dx` integrál egyszerre konvergens vagy divergens, de konvergens esetben a sor összegéről nem mond semmit. Viszont a feladat nem az egzakt összeget kéri, csak becslést. Ezt megtehetjük például úgy, hogy a sorösszeget minoráljuk és majoráljuk egy-egy konvergens integrállal. Lényegében a fordítottját csináljuk annak, amit a Riemann-integrál bevezetésénél szoktak: nem a görbe alatti területet szorítjuk alsó és felső téglalapok közé, hanem a téglalapok területét két görbe alatti terület közé.

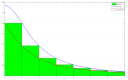
Mellékeltem egy képet. A zöld téglalapok területe a sor egyes tagjainak felel meg, tehát az összes zöld terület adja meg a sor összegét. A piros és a kék görbe alatti terület pedig nyilvánvalóan kisebb illetve nagyobb ennél a sorösszegnél, tehát ezek használhatók alsó és felső határnak:

`int_0^{oo}1/((x+1)^2+3) dx lt sum_{n=1}^{oo} 1/(n^2+3) lt int_0^{oo}1/(x^2+3) dx`

A felső becslés helyettesítéses integrálással (`u=1/sqrt(3) x``\ Rightarrow\ dx=sqrt(3) du`):

`int_0^{oo}1/(x^2+3) dx=``1/3 int_0^{oo}1/(x^2/3+1) dx=``1/3 sqrt(3) int_0^{oo}1/(u^2+1) du=``1/sqrt(3) [arctan u]_0^{oo}=``pi/(2sqrt(3))~~0.9069`

Az alsó becslés pedig ezt felhasználva:

`int_0^{oo}1/((x+1)^2+3) dx=``int_1^{oo}1/(x^2+3) dx=``1/sqrt(3) [arctan u]_{1/sqrt(3)}^{oo}=``1/sqrt(3)[pi/2-pi/6]=``pi/(3sqrt(3))~~0.6046`

A sor tényleges összege egyébként kb. `0.7403`, majdnem a két becslőnk átlaga.