1. A -1. hatvány azt jelenti, hogy a szám reciprokát vesszük, tehát:

2-1=1/2
3-1=1/3
2-2, ehhez a hatvány hatványozásának azonosságát használjuk, így kapjuk, hogy (2²)-1=4-1=1/4
Az utolsó tört egy vegyestört, ami kezelhető 1+(1/12) összegként, ennek az értéke (12/12)+(1/12)=13/12, ennek -1-edik hatványa 12/13.

Tehát ezt a műveletsort kell kiszámolnunk:

((1/2)+(1/3)+(1/4))*(12/13). Az első tényezőben közös nevezőre kell hozni. Jó közös nevező lesz a 12, ekkor az első törtet 6-tal, a másodikat 4-gyel, a harmadikat 3-mal bővítjük:

(6/12)+(4/12)+(3/12)=13/12, ezt kell még szoroznunk 12/13-dal:

(13/12)*(12/13)=156/156=1. Tehát a végeredmény 1 (egész).

2. Az "akasztófa" szerint felírjuk:
60|2
30|2
15|3
5|5
1, tehát 60=2*2*3*5=2²*3*5

3. Szorozzuk mindkét oldalt √3-mal, majd kivonunk 1-et:

x=((√3*√ 12 )/3)-1

√3*√ 12  értéke a gyökvonás azonossága szerint √ 3*12 =
√ 36 =6, tehát x=(6/3)-1=2-1=1.

4. Tetszőleges négyszög belső szögeinek összege 360°, így ha két szög összege 165°, akkor a másik két szög összege 195°.

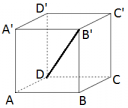
5. A kocka oldallapjai négyzetek, a négyzet átlói pedig 2 derékszögű háromszögre bontják a négyzetet ahol az átló az átfogó, ezért felírható a Pitagorasz-tétel; ha a lapátló hossza d, akkor:

5² + 5² =d², ennek megoldása √ 50 =d.

A kocka éle, lapátlója és testátlója szintén egy derékszögű háromszöget határoznak meg, ahol a testátló a testátló az átfogó; ha annak hossza D, akkor a tétel szerint:

5² + √ 50 ² =D², ennek megoldása √ 75  = D

Eszerint az arányuk: d : D= √ 50  : √ 75 . A két arányszám átírható a gyökvonás azonosságai szerint:
√ 50 =√ 25*2 =√ 25 *√2=5*√2
√ 75 =√ 25*3 =√ 25 *√3=5*√3

Tehát az arány felírható d : D= 5*√2 : 5*√3 alakban, itt viszont ha ugyanazzal a számmal osztjuk a számokat, akkor az arány nem változik, tehát √2 : √3 alakban is felírható az arány.

6. Összesen 72 m³ vizet fogyasztottak, így 72*4,85=349,2 lejt fizettek.

1. Mellékelve.

2. A 2,(3) azt jelenti, hogy 2,333.... Azzal már biztosan találkoztál, hogy 1/3=0,333..., tehát a 2,(3) értéke 2+(1/3)=(6/3)+(1/3)=7/3. Ha 1/3=0,333..., akkor 2/3=0,666..., tehát 6,(6)=6+(2/3)=(18/3)+(2/3)=20/3. A két szám összege (7/3)+(20/3)=(27/3)=9.

A √ 189  átírható √ 21*9 =√ 21 *√9=3*√ 21  alakban. Ebből kivonunk √ 21 -et, akkor 2*√ 21 -et kapunk, majd ezt visszaírva gyökös alakra: =√4*√ 21 =√ 4*21 =√ 84 .

A 9 gyökös alakja √ 81 . Azt tudjuk, hogy nagyobb szám gyöke is nagyobb, és mivel 81<84, ezért √ 81 <√ 84  is igaz lesz. Tehát x<y állítás igaz.

3. Ki tudunk emelni az összegből 3²⁰¹²-ent: 3²⁰¹²*(3²+3+1)=13*3²⁰¹², ez átírható 13*3*3²⁰¹¹=39*3²⁰¹¹ alakban. Ha ezt elosztjuk 39-cel, akkor 3²⁰¹¹-ent kapunk, ez egy egész szám, tehát az összeg tényleg osztható 39-cel.

4. Ennek több módon is neki lehet látni; az egyik megoldás ez:
Ha x≥0, akkor biztos, mert ha x=0, akkor a függvényérték 1, ha pedig x pozitív, akkor pozitív számok összege is pozitív lesz.
Most azt nézzük meg, hogy az x²+x≥0 mikor teljesül; kivonunk x-et, majd osztunk x-szel, de mivel most a negatív számok között keresgélünk, ezért fordul a reláció, tehát x≤-1-et kapjuk. Ebben az esetben x² pozitív, ebből ki kell vonni egy kisebb számot, (például ha x=-5, akkor (-5)²-5=25-5=20), ami így pozitív marad, ha pedig x=-1, akkor (-1)²-1=1-1=0, ehhez már kell a +1, hogy a függvényérték pozitív maradjon.
Ha -1<x<0, akkor x² értéke még mindig pozitív marad, viszont ha ebből kivonnánk x-et, akkor negatívba fordulna (például (-0,25)²-0,25=0,0625-0,25=-0,1875), viszont mivel -1<x<0 van, ezért x+1 értéke biztosan pozitív lesz, ha ehhez hozzáadjuk x², akkor még mindig pozitív marad.
Tehát a kifejezés értéke mindig pozitív lesz.

Ha tanultál már teljes négyzetes alakot, akkor azzal még egyszerűbb bizonyítani:

x²+x+1 = (x+0,5)²-0,5²+1 = (x+0,5)²-0,25+1 = (x+0,5)² + 0,75, (x+0,5)² értéke biztos, hogy legalább 0, így a függvényérték biztos, hogy legalább 0,75 lesz, tehát mindig nagyobb, mint 0.

5. Tegyük fel, hogy Anna életkora 4 évvel ezelőtt x volt, ekkor Péter életkora 6x. 4 évvel később Anna életkora x+4, Péteré 6x+4, itt Anna életkorának kétszerese lesz Péter életkora, tehát:

2*(x+4)=6x+4, ennek megoldása x=1. Tehát Anna 4 évvel ezelőtt 1, Péter 6 éves volt, most Anna 5 éves, Péter 10, 5*2=10, tehát jól számoltunk.

6. Ehhez egyenlővé kell őket tenni: √5*x+√5 = -√5*x+√5, egyenletrendezés után x=0 az eredménye. Ekkor a két függvény értéke √5, tehát a két függvény metszéspontja a (0;√5) pont.

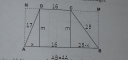
1a) Ehhez is csatoltam képet. A két magasság középen egy téglalapot vág ki, ezért lesz a hosszabbik alap középső részének hossza 16 cm, a másik két rész hossza így összesen 44-16=28 cm lesz. Ezen kívül kapunk még két derékszögű háromszöget is; ha a magasság m, a vízszintes befogó hossza x, akkor Pitagorasz tétele szerint:

x² + m² = 17², erre egyenletrendezés után m² = 289 - x² -et kapjuk.

A másik derékszögű háromszögben így a befogó hossza (28-x) lesz, így a tétel szerint:

(28-x)² + m² = 25², vagyis m² = 625 - (28-x)².

Mivel 289 - x² és 625 - (28-x)² értéke is m²-tel egyenlő, ezért kézenfekvő, hogy ezek egymással is egyenlőek, tehát:

289 - x² = 625 - (28-x)², kibontjuk a zárójeleket:
289 - x² = 625 - 784 + 56 x - x², ennek megoldása x=8, tehát a hosszabbik alap részei 8 és 20 cm hosszúak. A magasság: m²=289 - 8² = 289 - 64 = 225, ekkor m=15, tehát a trapéz magassága 15 cm.

b) A trapéz területe (44+16)*15/2=450 cm², a téglalap területe 15*44=660 cm², tehát a területek aránya 450 : 660, mindkét szám osztható 30-cal, így 15 : 22 alakban is megadható az arány.

c) A trapéz kerülete 44+25+16+17=102 cm, a téglalapé 44+15+44+15=118 cm, így a kettő különbsége 16 cm.

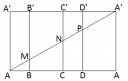
2a) Ehhez is csatoltam képet. Ha kiterítjük a síkba a palástot, akkor ezt kapjuk. Vegyük az AAA' derékszögű háromszöget, ahol az A-nál lévő hegyesszög 30°-os, az A'-nél lévő szög 60°-os, mivel tetszőleges háromszögben a belső szögek összeg 180°, és 30°+60°+90°=180°. Ha ezt tükrözzük az AA oldalra, akkor egy egyenlő szárú háromszöget kapunk, ahol minden belső szög 60°-os, vagyis ez a háromszög egyben szabályos háromszög is lesz, vagyis minden oldala 32 méter hosszú. A tükörtengely felezi az oldalakat, ezért a függőleges AA' szakasz hossza 16 méter lesz, így az oszlop magassága is.

b) Pitagorasz tétele szerint az AA oldal hossza:

(AA)² + 16² = 32², tehát AA=√ 768 , tehát √ 768  méter hosszú. A palást területe az AAA'A' téglalap területével egyezik meg, ami így 16*√ 768  m², ami kerekítve 443,405 m².

c) Ezen még gondolkodnom kell egy kicsit.

Valami miatt nem csatolódtak a képek...