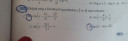Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Fontos!
 Denver
kérdése
Denver
kérdése
397
Rövid határidő! Ma éjfél! Előre is köszönöm a segítséget!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 Ármós Csaba
megoldása
Ármós Csaba
megoldása
5235. feladat: Legyen a találkozásig y km a megtett útja mindkét vonatnak. Az egyik sebességére felírható, hogy: 30=y/(x vessző), a másikra pedig 80=y/(x vessző-3), az y értékek megegyeznek (találkozásukig megtett utak egyenlőek), így az írható fel, hogy 30×(x vessző)=80×(x vessző-3), melyből az x vessző-re 4,8 óra fog kijönni. A gyorsvonat (Intercity) ideje tehát 1,8 óra, ami 1 óra 48 percet jelent, tehát ezt a 8 órához hozzá kell adni, így kapjuk, hogy 9 óra 48 perckor fog a két vonat találkozni!  A megtett út pedig : y= 30×4,8= 144 km lesz!
A megtett út pedig : y= 30×4,8= 144 km lesz!
5249. feladat: pi/4=45 fok, ezért (x-45 fok) vagy egyenlő 135 fok + k× 360 fok-kal, vagy pedig egyenlő 225 fok + l× 360 fokkal. Előzőből kapjuk, hogy x(1) = (180 fok + k× 360) fok, ill. x(2) = (270 fok + l× 360 fok)! Ezek lesznek a megoldások! A 360 fok a sin és cos periódusát jelenti!
Ezek lesznek a megoldások! A 360 fok a sin és cos periódusát jelenti!  Két megoldás van!
Két megoldás van!
A másik egyenletből: (2x- 180 fok)= 60 fok+ k× 180 fok, vagyis 2x = 240 fok + k× 180 fok, kettővel osztjuk a szöget és a periódust is, így kapjuk meg a megoldást: x = (120 fok + k× 90 fok)! Itt csak ez az egy megoldás van!
Itt k, l egész számok (lehet pozitív vagy negatív, sőt nulla is), ill. a tangensfüggvény periódusa nem 360 fok, hanem 180 fok!
5280. feladat: b; y=m × x + b az általános képlet ( x a pont 1. koordinátája, y a pont 2. koordinátája, m a függvény meredeksége és b a tengelymetszete), így: A pont miatt b=-2 lesz, a másik egyenlet a B pontra felírva 1= 2m-2, tehát ebből az m=1,5 lesz! Így a függvény képlete: y=1,5x-2 lehet csak!
d; pont : Az előzőeket figyelembevéve itt az A pontból b=0 és a B pontból -3= m×1, vagyis m=-3 adódik! Így a függvény képlete: y=-3×x + 0 = (-3x) lesz!
c; pont: Az y értéke mindkettőnél 3, ezért b-re felírhatjuk a következő egyenletet: b-5m = b+7m, melyből 12m=0, vagyis m=0 (a függvény meredeksége nulla), és 3=0×x + b képletből b=3 adódik. Így a függvény egyenlete: y=3 lesz (konstans függvény) !
Remélem így már érted is a leírt megoldásokat!
 A megtett út pedig : y= 30×4,8= 144 km lesz!
A megtett út pedig : y= 30×4,8= 144 km lesz!5249. feladat: pi/4=45 fok, ezért (x-45 fok) vagy egyenlő 135 fok + k× 360 fok-kal, vagy pedig egyenlő 225 fok + l× 360 fokkal. Előzőből kapjuk, hogy x(1) = (180 fok + k× 360) fok, ill. x(2) = (270 fok + l× 360 fok)!
 Ezek lesznek a megoldások! A 360 fok a sin és cos periódusát jelenti!
Ezek lesznek a megoldások! A 360 fok a sin és cos periódusát jelenti!  Két megoldás van!
Két megoldás van!A másik egyenletből: (2x- 180 fok)= 60 fok+ k× 180 fok, vagyis 2x = 240 fok + k× 180 fok, kettővel osztjuk a szöget és a periódust is, így kapjuk meg a megoldást: x = (120 fok + k× 90 fok)! Itt csak ez az egy megoldás van!
Itt k, l egész számok (lehet pozitív vagy negatív, sőt nulla is), ill. a tangensfüggvény periódusa nem 360 fok, hanem 180 fok!
5280. feladat: b; y=m × x + b az általános képlet ( x a pont 1. koordinátája, y a pont 2. koordinátája, m a függvény meredeksége és b a tengelymetszete), így: A pont miatt b=-2 lesz, a másik egyenlet a B pontra felírva 1= 2m-2, tehát ebből az m=1,5 lesz! Így a függvény képlete: y=1,5x-2 lehet csak!
d; pont : Az előzőeket figyelembevéve itt az A pontból b=0 és a B pontból -3= m×1, vagyis m=-3 adódik! Így a függvény képlete: y=-3×x + 0 = (-3x) lesz!
c; pont: Az y értéke mindkettőnél 3, ezért b-re felírhatjuk a következő egyenletet: b-5m = b+7m, melyből 12m=0, vagyis m=0 (a függvény meredeksége nulla), és 3=0×x + b képletből b=3 adódik. Így a függvény egyenlete: y=3 lesz (konstans függvény) !

Remélem így már érted is a leírt megoldásokat!

Módosítva: 4 éve
0
- Még nem érkezett komment!