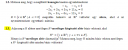Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Merőleges altér
 Lola19
kérdése
Lola19
kérdése
387
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
2 gyula205
válasza
gyula205
válasza
Tulajdonképpen a feladat második része triviális. Bármelyik elemét is vesszük elő `H`-nak, az merőleges lesz `H^(bot)` minden elemére. Ez igaz lesz a bázisvektorokra is. Az első résznél befogjuk bizonyítani, hogy a két érintett `H` és `H^(bot)` altér kifeszíti az egész teret és metszetük 0 vektor. Másodszor be fogjuk látni, hogy `H=(H^(bot))^(bot)` állítás is igaz lesz.
1/1 esetén legyen `e_1, e_2 ,... e_r` a `H` altér ortonormált bázisa, majd vegyük elő a `N` tér tetszőleges `u` vektorát, és legyen `e=(u;e_1)e_1+(u;e_1)e_1+...(u;e_r)e_r`. A bázisvektorok ortonormáltsága alapján `(e;e_i)=(u;e_i) (i=1, 2,...r)`, azaz `(u-e;e_i)=0`, azaz `v=u-e in H^(bot)`.
Így a tér `u` vektora `u=v+e` alakba írható, ahol `e in H`. Ha `t` vektor eleme a metszetnek, akkor eleme a `H^(bot)`-nak is, így merőleges `H` minden elemére is, azaz önmagára is. `(t;t)=0 ` A pozitív definit tulajdonság alapján `t=0`.
1/2 Ha `u in H`, akkor `u` merőleges `H^(bot)` minden elemére, amiből következik, hogy
` u in (H^(bot))^(bot)`. 1/1-ből `N=H+H^(bot)` valamint 1/2 első részéből, ahol a "`+`" jel a két altér direkt összegére utal.
`N=H^(bot)+(H^(bot))^(bot)`. Így` H=(H^(bot))^(bot)`. a két altér dimenziója azonos.
1/3. Már csak a a dimenziók közti összefüggést kell felhasználni: `dim(N)=dim(H)+dim(H^(bot))-dim(N_0)`, ahol `N_0` a zéróaltérre utal, aminek dimenziója éppen 0. Kellett, hogy tanuljátok, hogy ha `L_1` és `L_2` két altere a `N`-nek, továbbá magát az `N` teret is altérnek tekintve és `N_0= L_1 cap L2` igaz a következő összefüggés: `dim(N)=dim(L_1)+dim(L_2)-dim(N_0)`. Így
speciális esetben `dim(H)+dim(H^(bot))=4`.
Most látom, hogy 1.3 feladat összefüggésben van 1.2 feladattal. Így a megoldás során konkrét számadatokat kellene prezentálni. Jó neked az ha az igazi megoldás késik mondjuk 24 órát? Most nekem más irányú feladataim is volnának...
1/1 esetén legyen `e_1, e_2 ,... e_r` a `H` altér ortonormált bázisa, majd vegyük elő a `N` tér tetszőleges `u` vektorát, és legyen `e=(u;e_1)e_1+(u;e_1)e_1+...(u;e_r)e_r`. A bázisvektorok ortonormáltsága alapján `(e;e_i)=(u;e_i) (i=1, 2,...r)`, azaz `(u-e;e_i)=0`, azaz `v=u-e in H^(bot)`.
Így a tér `u` vektora `u=v+e` alakba írható, ahol `e in H`. Ha `t` vektor eleme a metszetnek, akkor eleme a `H^(bot)`-nak is, így merőleges `H` minden elemére is, azaz önmagára is. `(t;t)=0 ` A pozitív definit tulajdonság alapján `t=0`.
1/2 Ha `u in H`, akkor `u` merőleges `H^(bot)` minden elemére, amiből következik, hogy
` u in (H^(bot))^(bot)`. 1/1-ből `N=H+H^(bot)` valamint 1/2 első részéből, ahol a "`+`" jel a két altér direkt összegére utal.
`N=H^(bot)+(H^(bot))^(bot)`. Így` H=(H^(bot))^(bot)`. a két altér dimenziója azonos.
1/3. Már csak a a dimenziók közti összefüggést kell felhasználni: `dim(N)=dim(H)+dim(H^(bot))-dim(N_0)`, ahol `N_0` a zéróaltérre utal, aminek dimenziója éppen 0. Kellett, hogy tanuljátok, hogy ha `L_1` és `L_2` két altere a `N`-nek, továbbá magát az `N` teret is altérnek tekintve és `N_0= L_1 cap L2` igaz a következő összefüggés: `dim(N)=dim(L_1)+dim(L_2)-dim(N_0)`. Így
speciális esetben `dim(H)+dim(H^(bot))=4`.
Most látom, hogy 1.3 feladat összefüggésben van 1.2 feladattal. Így a megoldás során konkrét számadatokat kellene prezentálni. Jó neked az ha az igazi megoldás késik mondjuk 24 órát? Most nekem más irányú feladataim is volnának...
Módosítva: 4 éve
0
-
Lola19: Köszönöm a választ! Igazság szerint mára kellene 4 éve 0
-
gyula205: Ok. Megpróbálom a megoldást 16.00-ig befejezni. 4 éve 0
 gyula205
megoldása
gyula205
megoldása
Ha megoldjuk az 1.2 egyenletet, akkor `(z+t; -(z+3t); z; t)` kétparaméteres vektor sokaságot kapjuk megoldásként.
Ebből összeállítunk egy négyzetes mátrixot:
`[[t,z,2,z+t],[-3t, -z, -4, -(z+3t)],[0, z, 1, z],[t, 0,1, t]]` aminek a rangja `2`, tehát biztosan lesz `2` lineárisan független oszlopvektor, akárhogy is választunk ki 3 oszlopvektort. Ugyanez az állítás kimondható a sorvektorokra is. Ez azt fogja jelenteni, hogy `dim(H)=2`.
Ha felvesszük `tz=-1` feltételt, akkor a két utolsó sor ortogonális lesz és a `z=-frac{1}{t}` feltételt, akkor `[[t,-1/t,2,-1/t+t],[-3t, 1/t, -4, 1/t-3t],[0, -1/t, 1, -1/t],[t, 0,1, t]]` egyparaméteres mátrixhoz jutunk (`t ne 0`), amelynek utolsó két sora ortogonális. `xi` és `eta`-val jelölve a két utolsó sorvektort, `-xi-3eta` valamint `xi+eta` előllítja az első két sorvektort is.
Az `abs(xi)=frac{sqrt(2+t^2)}{t}` valamint `abs(eta)=sqrt(2t^2+1)` normával ezek ortonormáltá , azaz bázisvektorokká tehetők a `H` altéren.
Tudjuk azt, hogy `dim(H^(bot))=2`. Keressük azt a két `lambda` és `mu` vektorokat, hogy `lambda*mu=0` és `lambda*xi=0`, `lambda*eta=0`, `xi*mu=0` valamint `eta*mu=0` legyen. Keressük a megoldásokat `lambda=(a; b; c; 1)` és `mu=(u; v; 1; 0)` alakban. A megoldás a következő alakokat hozza: `a=frac{-t^2(t^2+2)}{t^4+t^2+1}`, `b=-frac{2t^2+1}{t^4+t^2+1}`, `c=frac{t(t^2-1)}{t^4+t^2+1}`, `u=-1/t` és `v=t`. Normálás után a kapott két vektor szintén bázisvektorokká tehetők a `H^(bot)` altéren.
Ebből összeállítunk egy négyzetes mátrixot:
`[[t,z,2,z+t],[-3t, -z, -4, -(z+3t)],[0, z, 1, z],[t, 0,1, t]]` aminek a rangja `2`, tehát biztosan lesz `2` lineárisan független oszlopvektor, akárhogy is választunk ki 3 oszlopvektort. Ugyanez az állítás kimondható a sorvektorokra is. Ez azt fogja jelenteni, hogy `dim(H)=2`.
Ha felvesszük `tz=-1` feltételt, akkor a két utolsó sor ortogonális lesz és a `z=-frac{1}{t}` feltételt, akkor `[[t,-1/t,2,-1/t+t],[-3t, 1/t, -4, 1/t-3t],[0, -1/t, 1, -1/t],[t, 0,1, t]]` egyparaméteres mátrixhoz jutunk (`t ne 0`), amelynek utolsó két sora ortogonális. `xi` és `eta`-val jelölve a két utolsó sorvektort, `-xi-3eta` valamint `xi+eta` előllítja az első két sorvektort is.
Az `abs(xi)=frac{sqrt(2+t^2)}{t}` valamint `abs(eta)=sqrt(2t^2+1)` normával ezek ortonormáltá , azaz bázisvektorokká tehetők a `H` altéren.
Tudjuk azt, hogy `dim(H^(bot))=2`. Keressük azt a két `lambda` és `mu` vektorokat, hogy `lambda*mu=0` és `lambda*xi=0`, `lambda*eta=0`, `xi*mu=0` valamint `eta*mu=0` legyen. Keressük a megoldásokat `lambda=(a; b; c; 1)` és `mu=(u; v; 1; 0)` alakban. A megoldás a következő alakokat hozza: `a=frac{-t^2(t^2+2)}{t^4+t^2+1}`, `b=-frac{2t^2+1}{t^4+t^2+1}`, `c=frac{t(t^2-1)}{t^4+t^2+1}`, `u=-1/t` és `v=t`. Normálás után a kapott két vektor szintén bázisvektorokká tehetők a `H^(bot)` altéren.
Módosítva: 4 éve
1
- Még nem érkezett komment!