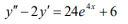Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Analízis differenciálegyenlet próbafüggvénnyel
 kisvarga2001
kérdése
kisvarga2001
kérdése
357
Oldja meg az állandó együtthatós differenciálegyenletet próbafüggvény
módszerrel!
módszerrel!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Nézzük a homogén részt: `y_h''-2y_h'=0`. A megoldások `e^(lambda x)` alakúak lesznek, helyettesítsük ezt be:
`lambda^2 e^(lambda x) -2lambda e^(lambda x)=0`
`lambda^2-2lambda=0`
A kapott karakterisztikus egyenletnek két különböző valós megoldása van (`lambda_1=2` és `lambda_2=0`), tehát a homogén rész megoldása:
`y_h(x)=C_1 e^(lambda_1 x)+C_2 e^(lambda_2 x)=``C_1 e^(2 x)+C_2`
Az inhomogén egyenlethez a próbafüggvényünk legyen `y_p(x)=C_3 e^{4x}+C_4x` (a homogén rész sajátértékeitől eltérő a gerjesztés kitevője, tehát rezonanciával nem kell számolnunk). Helyettesítsük ezt be:
`16C_3 e^{4x}-8C_3e^{4x}-2C_4=24e^{4x}+6`
Innen a konstansok: `C_3=3` és `C_4=-3`.
A teljes általános megoldás tehát: `y(x)=3e^{4x}-3x+C_1 e^{2x}+C_2`
`lambda^2 e^(lambda x) -2lambda e^(lambda x)=0`
`lambda^2-2lambda=0`
A kapott karakterisztikus egyenletnek két különböző valós megoldása van (`lambda_1=2` és `lambda_2=0`), tehát a homogén rész megoldása:
`y_h(x)=C_1 e^(lambda_1 x)+C_2 e^(lambda_2 x)=``C_1 e^(2 x)+C_2`
Az inhomogén egyenlethez a próbafüggvényünk legyen `y_p(x)=C_3 e^{4x}+C_4x` (a homogén rész sajátértékeitől eltérő a gerjesztés kitevője, tehát rezonanciával nem kell számolnunk). Helyettesítsük ezt be:
`16C_3 e^{4x}-8C_3e^{4x}-2C_4=24e^{4x}+6`
Innen a konstansok: `C_3=3` és `C_4=-3`.
A teljes általános megoldás tehát: `y(x)=3e^{4x}-3x+C_1 e^{2x}+C_2`
0
- Még nem érkezett komment!