A 18 b) feladat gondolat-menete:

a) Ez a gráfban azt jelenti, hogy a gráf minden csúcsának fokszáma ugyanannyi, tehát lehet 0;1;2;3;4;5;6 a lejátszott meccsek száma, de mivel "még javában folytak a meccsek", ezért a 6 kiesik, és ebből a megfogalmazásból azért érezhető, hogy már valamennyi meccset lejátszottak, ezért a 0 is. Azt is tudjuk a gráfokról, hogy minden gráfban a fokszámösszeg páros, és mivel 7 versenytő van, ezért az összeg csak úgy lehet páros, hogyha páros sok mérkőzés ment le, tehát vagy 2, vagy 4 mérkőzést játszott mindenki.

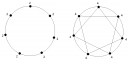
Olyan gráfot mindenki tud rajzolni, ahol minden csúcs fokszáma 2; körbe-körbe összekötjük őket. A 4 fokszámút például úgy kaphatjuk meg, hogy körbe mindenkit összekötünk, majd minden másodikat, amíg vissza nem jutunk az elsőhöz (természetesen máshogyan is lehet kötögetni, de talán ez a legegyszerűbb).

b) Minden játékos 6 másikkal játszott, vagyis emberenként 7*6=42 mérkőzést számolhatunk meg, viszont minden mérkőzés mindkét félnél meg lett számolva, ezért a kapott számot el kell osztanunk 2-vel, így 42/2=21 mérkőzést játszottak.

c) Akármi is lett a parti végkimenetele, az biztos, hogy az összpontszám 1-gyel nőtt, tehát 21 pont lett kiosztva összesen. Tegyük fel, hogy a 4. ember pontszáma x, a helyezettek közti különbség d, ekkor a pontok felírhatóak növekvő sorrendben x-3d ; x-2d ; x-d ; x ; x+d; x+2d; x+3d alakban, ezek összege pont 21, tehát:

(x-3d)+(x-2d)+(x-d)+x+(x+d)+(x+2d)+(x+3d)=21, a zárójeleknek igazából csak annyi funkciójuk van, hogy azok tartoznak össze. Mindenesetre látjuk, hogy a d-k megeszik egymást, így marad:

7x=21, erre x=3 adódik. Ez azt jelenti, hogy d értéke elméletben bármennyi lehet, gyakorlatban viszont annak teljesülnie kell, hogy minden pontszám vagy egész vagy egész+0,5 alakú kell, hogy legyen, illetve senki sem kaphatott 0-nál kevesebb és 6-nál több pontot, emiatt d értéke legfeljebb 1 lehet, így d értékére 3 lehetőség van:

1. d=0, ekkor a pontszámok: 3;3;3;3;3;3;3, ez például úgy lehet, hogy mindenki mindenkivel döntetlent játszott.
2. d=0,5, ekkor 1,5;2;2,5;3;3,5;4;4,5, ez például úgy lehet, hogy akiknek van fél pontjuk, azok közül 2-2 döntetlent játszott, a többi partiban valaki nyert.
3. d=1, ekkor 0;1;2;3;4;5;6 pontszámok születhettek, ez például úgy lehet, hogy mindenki azokat győzte le, akiknél több pontot szerzett.

(Ha esetleg a fenti trükköt nem ismerjük, és a tanultak szerint az x+(x+d)+(x+2d)+(x+3d)+(x+4d)+(x+5d)+(x+6d)=21 alakban írjuk fel az egyenletet, akkor is kijön, csak kicsit másként; összevonás után 7x+21d=21 egyenletet kapjuk, ezt osztjuk 7-tel, így az x+3d=3 egyenlethez jutunk, itt pedig láthatjuk, hogy az x+3d eredetileg a 4. ember pontszáma volt.)