Ha jól értem, akkor valami ilyesmiről van szó:

http://www.vasutmodell-centrum.hu/terepepites/hidak/faller-120536-vasuti-ivbordas-hid-360-mm-p-3150-74-22.html?utm_source=termek-kartya&utm_medium=termek_kep&utm_term=termek-Faller%20120536&utm_campaign=termekkartyarol-adatlapra

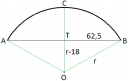
Ebben az esetben tekinthetjük a hidat egy körszeletnek, melynek húrhossza 125 méter, magassága (vagyis a húrra merőleges szakaszok közül a leghosszabb szakasz hossza) 18 méter (1. ábra), ennek az ívhossza a kérdés, amit a hozzá tartozó kör sugarából és a középponti szög nagyságából tudunk meghatározni.

Jelöljük ki a kör középpontját, és kössük össze a körszelet végpontjaival, ezek lesznek a kör sugarai (a zöldek). Látható, hogy ekkor keletkezett egy OAB egyenlő szárú háromszög, melynek szárainak hossza így r méter, alapja 125 méter. Az OT szakasz merőleges az AB szakaszra, ezért az az OAB egyenlő szárú háromszöget két derékszögű háromszögre bontja, amik egyenlő szárú háromszög esetén egybevágóak. Ebben az OTB derékszögű háromszögben az átfogó hossza r méter, befogója 62,5 méter (mivel 125/2=62,5), másik befogójának hossza r-18 méter hosszú, mivel a TC szakasz hossza 18 méter, az OC szakasz hossza r méter, ezért ezek különbsége, tehát r-18 méter lesz az OT szakasz hossza. Erre a derékszögű háromszögre fel tudjuk írni Pitagorasz tételét:

62,5²+(r-18)²=r², ennek megoldása r=16921/144 méter (a törtet szeretem olyan alakban megadni, hogy két egész szám hányadosa, amik relatív prímek egymáshoz).

Ennek ismeretében ki kell számolnunk a körívhez tartozó középponti szöget, vagyis az AOB szög nagysága érdekel most minket, azt pedig a derékszögű háromszögből tudjuk kiszámolni úgy, hogy az O-nál lévő szögére (ez legyen α) felírjuk valamelyik szögfüggvényt, például a szinuszát, ekkor:

sin(α)=62,5/(16921/144)=9000/16921, ennek megoldása α=arcsin(9000/16921)°. Mivel az OT szakasz felezi az AOB szöget, és a félszög α, ezért az AOB szög nagysága 2*arcsin(9000/16921)°.

Tudjuk, hogy az r sugarú, α középponti szögű körív hossza 2*r*π*α/360°, tehát ennek a hossza 2*(16921/144)*π*2*arcsin(9000/16921)°/360° méter, igény szerint lehet kerekíteni.