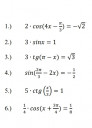Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Trigonometrikus egyenletek
 zs_adele
kérdése
zs_adele
kérdése
442
Nem vagyok biztos a megoldásokba meg pár dolog menetével.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 Nagy-Gombás Szilvi
{ Tanár }
megoldása
Nagy-Gombás Szilvi
{ Tanár }
megoldása
1. feladat:
2 * cos(4x - π/3) =-√ 2 / : 2
cos(4x- π/3) = -√ 2 /2
( cos 45⁰ = cos π/4 = √ 2 /2 )
1. megoldás: (II. síknegyed) a - előjel miatt
4x - π/3 = π - π/4 + k * 2π / * 12
48x - 4π = 12π - 3π + k * 24π
48x - 4π = 9π + k * 24π / + 4π
48x = 13π + k * 24π / : 48
x = 13π/48 + k * π/2 (k ε Z)
2. megoldás: (III. síknegyed)
4x - π/3 = π + π/4 + k * 2π / * 12
48x - 4π = 12π + 3π + k * 24π
48x - 4π = 15π + k * 24π / + 4π
48x = 19π + k * 24π / : 48
x = 19π/48 + k * π/2 (k ε Z)
2. feladat:
3 * sinx = 1 / : 3
sinx = 1/3 = 0,3334
( sin19,47⁰ = 1/3 )
1. megoldás: (I. síknegyed)
x = 19,47⁰ + k * 360⁰ (k ε Z)
2. megoldás: (II. síknegyed)
x = 180⁰ - 19,47⁰ + k * 360⁰
x = 160,53⁰ + k - 360⁰ (k ε Z)
3. feladat:
3 * tg(π - x) = √ 3
Értelmezési tartomány:
π - x ≠ π/2 + k * π / - π
-x ≠ -π/2 + k * π / : (-1)
x ≠ π/2 - k * π
3 * tg(π - x) = √ 3 / : 3
tg(π - x) = √ 3 /3
( tg 30⁰ = tg π/6 = √ 3 /3 )
π - x = π/6 + k * π / - π
-x = π/6 - π + k * π
-x = π/6 - 6π/6 + k * π
-x = -5π/6 + k * π / : (-1)
x = 5π/6 - k * π (k ε Z)
4. feladat:
sin(2π/3 - 2x) = -1/2
( sin 30⁰ = sin π/6 = 1/2 )
1. megoldás: (III. siknegyed) a - előjel miatt
2π/3 - 2x = π + π/6 + k * 2π / * 6
4π - 12x = 6π + π + k * 12π
4π - 12x = 7π + k * 12π / - 4π
-12x = 3π + k * 12π / : (-12)
x = -π/4 - k * π (k ε Z)
2. megoldás: (IV. síknegyed)
2π/3 - 2x = 2π - π/6 + k * 2π / * 6
4π - 12x = 12π - π + k * 12π
4π - 12x = 11π + k * 12π / - 4π
-12x = 7π + k * 12π / : (-12)
x = -7π/12 - k * π (k ε Z)
5. feladat:
5 * ctg(x/3) = 1
Értelmezési tartomány:
x/3 ≠ 0 + k * π / * 3
x ≠ 0 + k * 3π
5 * ctg(x/3) = 1 / : 5
ctg(x/3) = 1/5 (= 0,2)
( ctg 78,69⁰ = 1/5 )
x/3 = 78,69⁰ + k * 180⁰ / * 3
x = 236,07⁰ + k * 540⁰ (k ε Z)
6. feladat:
1/4 * cos(x + 3π/4) = 1/8 / * 4
cos(x + 3π/4) = 1/2
( cos 60⁰ = cos π/3 = 1/2 )
1. megoldás: (I. síknegyed)
x + 3π/4 = π/3 + k * 2π / * 12
12x + 9π = 4π + k * 24π / - 9π
12x = -5π + k * 24π / : 12
x = -5π/12 + k * 2π (k ε Z)
2. megoldás: (IV. síknegyed)
x + 3π/4 = 2π - π/3 + k * 2π / * 12
12x + 9π = 24π - 4π + k * 24π
12x + 9π = 20π + k * 24π / - 9π
12x = 11π + k * 24π / : 12
x = 11π/12 + k * 2π (k ε Z)
2 * cos(4x - π/3) =-√ 2 / : 2
cos(4x- π/3) = -√ 2 /2
( cos 45⁰ = cos π/4 = √ 2 /2 )
1. megoldás: (II. síknegyed) a - előjel miatt
4x - π/3 = π - π/4 + k * 2π / * 12
48x - 4π = 12π - 3π + k * 24π
48x - 4π = 9π + k * 24π / + 4π
48x = 13π + k * 24π / : 48
x = 13π/48 + k * π/2 (k ε Z)
2. megoldás: (III. síknegyed)
4x - π/3 = π + π/4 + k * 2π / * 12
48x - 4π = 12π + 3π + k * 24π
48x - 4π = 15π + k * 24π / + 4π
48x = 19π + k * 24π / : 48
x = 19π/48 + k * π/2 (k ε Z)
2. feladat:
3 * sinx = 1 / : 3
sinx = 1/3 = 0,3334
( sin19,47⁰ = 1/3 )
1. megoldás: (I. síknegyed)
x = 19,47⁰ + k * 360⁰ (k ε Z)
2. megoldás: (II. síknegyed)
x = 180⁰ - 19,47⁰ + k * 360⁰
x = 160,53⁰ + k - 360⁰ (k ε Z)
3. feladat:
3 * tg(π - x) = √ 3
Értelmezési tartomány:
π - x ≠ π/2 + k * π / - π
-x ≠ -π/2 + k * π / : (-1)
x ≠ π/2 - k * π
3 * tg(π - x) = √ 3 / : 3
tg(π - x) = √ 3 /3
( tg 30⁰ = tg π/6 = √ 3 /3 )
π - x = π/6 + k * π / - π
-x = π/6 - π + k * π
-x = π/6 - 6π/6 + k * π
-x = -5π/6 + k * π / : (-1)
x = 5π/6 - k * π (k ε Z)
4. feladat:
sin(2π/3 - 2x) = -1/2
( sin 30⁰ = sin π/6 = 1/2 )
1. megoldás: (III. siknegyed) a - előjel miatt
2π/3 - 2x = π + π/6 + k * 2π / * 6
4π - 12x = 6π + π + k * 12π
4π - 12x = 7π + k * 12π / - 4π
-12x = 3π + k * 12π / : (-12)
x = -π/4 - k * π (k ε Z)
2. megoldás: (IV. síknegyed)
2π/3 - 2x = 2π - π/6 + k * 2π / * 6
4π - 12x = 12π - π + k * 12π
4π - 12x = 11π + k * 12π / - 4π
-12x = 7π + k * 12π / : (-12)
x = -7π/12 - k * π (k ε Z)
5. feladat:
5 * ctg(x/3) = 1
Értelmezési tartomány:
x/3 ≠ 0 + k * π / * 3
x ≠ 0 + k * 3π
5 * ctg(x/3) = 1 / : 5
ctg(x/3) = 1/5 (= 0,2)
( ctg 78,69⁰ = 1/5 )
x/3 = 78,69⁰ + k * 180⁰ / * 3
x = 236,07⁰ + k * 540⁰ (k ε Z)
6. feladat:
1/4 * cos(x + 3π/4) = 1/8 / * 4
cos(x + 3π/4) = 1/2
( cos 60⁰ = cos π/3 = 1/2 )
1. megoldás: (I. síknegyed)
x + 3π/4 = π/3 + k * 2π / * 12
12x + 9π = 4π + k * 24π / - 9π
12x = -5π + k * 24π / : 12
x = -5π/12 + k * 2π (k ε Z)
2. megoldás: (IV. síknegyed)
x + 3π/4 = 2π - π/3 + k * 2π / * 12
12x + 9π = 24π - 4π + k * 24π
12x + 9π = 20π + k * 24π / - 9π
12x = 11π + k * 24π / : 12
x = 11π/12 + k * 2π (k ε Z)
0
-
zs_adele: köszönöm szépen 5 éve 0