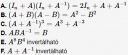Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Válaszd ki az össze állítást, mely igaz minden n×n-es A és B invertálható mátrixra.
gabor.schuh
kérdése
235
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1
AlBundy
{ Polihisztor }
megoldása
A) Igaz, a mátrixszorzás az összeadásra nézve disztributív.
B) Általánosan nem igaz, csak ha `\mathbf{A}` és `\mathbf{B}` kommutál, azaz `\mathbf{AB}=\mathbf{BA}`.
C) Nem igaz: `(\mathbf{A}+\mathbf{A}^-1)^3=``\mathbf{A}^3+ 3\mathbf{A} + 3 \mathbf{A}^-1 + \mathbf{A}^-3`
D) Nem igaz, a mátrixszorzás nem kommutatív.
E) Igaz, `(\mathbf{A}^8 \mathbf{B}^4)^-1=\mathbf{B}^-4 \mathbf{A}^-8`.
F) Nem igaz. Ellenpélda: `\mathbf{A}=[[i,0],[0,i]]`. Ekkor `\mathbf{A}^-1=[[-i,0],[0,-i]]`, tehát `\mathbf{A}+\mathbf{A}^-1=\mathbf{0}`, ami nem invertálható.
B) Általánosan nem igaz, csak ha `\mathbf{A}` és `\mathbf{B}` kommutál, azaz `\mathbf{AB}=\mathbf{BA}`.
C) Nem igaz: `(\mathbf{A}+\mathbf{A}^-1)^3=``\mathbf{A}^3+ 3\mathbf{A} + 3 \mathbf{A}^-1 + \mathbf{A}^-3`
D) Nem igaz, a mátrixszorzás nem kommutatív.
E) Igaz, `(\mathbf{A}^8 \mathbf{B}^4)^-1=\mathbf{B}^-4 \mathbf{A}^-8`.
F) Nem igaz. Ellenpélda: `\mathbf{A}=[[i,0],[0,i]]`. Ekkor `\mathbf{A}^-1=[[-i,0],[0,-i]]`, tehát `\mathbf{A}+\mathbf{A}^-1=\mathbf{0}`, ami nem invertálható.
0
- Még nem érkezett komment!