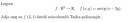Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Másodrendű Taylor polinom
 Zhaj
kérdése
Zhaj
kérdése
1283
Másodrendű Taylor polinom
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 bongolo
{
bongolo
{  }
megoldása
}
megoldása
Két változó van, itt majd parciális deriváltakat kell csinálni.
Másodrendű, vagyis második deriváltig kell elmenni.
Általánosságban így van a Taylor az (a,b) pont körül:
f(a,b) + (x-a)·fx(a,b) + (y-b)·fy(a,b) + 1/2! · ((x-a)²·fxx(a,b) + 2(x-a)(x-b)·fxy + (y-b)²·fyy(a,b))
Az alsó index x illetve y azt jelenti, hogy olyan parciális derivált kell.
fx = ∂/∂x arctg(x-2y) = 1 / [(x-2y)² + 1]
fy = ∂/∂y arctg(x-2y) = -2 / [(x-2y)² + 1]
fxy = ∂²/∂x∂y arctg(x-2y) = ∂/∂y 1 / [(x-2y)² + 1] = (-1 / [(x-2y)² + 1]² ) · 2·(x-2y)·(-2) = 4·(x-2y) / [(x-2y)² + 1]²
A maradék két deriváltat csináld meg te...
Aztán be kell persze helyettesíteni (3, 1)-et...
Ugye menni fog?
Másodrendű, vagyis második deriváltig kell elmenni.
Általánosságban így van a Taylor az (a,b) pont körül:
f(a,b) + (x-a)·fx(a,b) + (y-b)·fy(a,b) + 1/2! · ((x-a)²·fxx(a,b) + 2(x-a)(x-b)·fxy + (y-b)²·fyy(a,b))
Az alsó index x illetve y azt jelenti, hogy olyan parciális derivált kell.
fx = ∂/∂x arctg(x-2y) = 1 / [(x-2y)² + 1]
fy = ∂/∂y arctg(x-2y) = -2 / [(x-2y)² + 1]
fxy = ∂²/∂x∂y arctg(x-2y) = ∂/∂y 1 / [(x-2y)² + 1] = (-1 / [(x-2y)² + 1]² ) · 2·(x-2y)·(-2) = 4·(x-2y) / [(x-2y)² + 1]²
A maradék két deriváltat csináld meg te...
Aztán be kell persze helyettesíteni (3, 1)-et...
Ugye menni fog?
Módosítva: 8 éve
1
- Még nem érkezett komment!