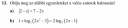Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Próbaérettségi feladatban volt ez a két feladat
 Vera
kérdése
Vera
kérdése
290
A képen vannak a feladatok
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
4 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
≥a)
|2 - x| = 7 - 2x
Az abszolútérték definíciója szerint nemnegatív szám abszolútértéke mag,a a szám, negatív szám abszolútértéke pedig a szám pozitív ellentettjével (-1-szeresével) egyenlő.
Ezért két esetet kell vizsgálni.
I. eset: (amikor az abszolútértékben levő szám nemnegatív, azaz ≥ 0)
Tehát 2 - x ≥ 0
2 ≥ x vagy intervallummal x ε ] - végtelen ; 2 ] esetén:
2 - x = 7 - 2x / + 2x
2 + x = 7 / - 2
x = 5 Nem megoldás, mert nincs benne az értelmezési tartományban. 2 ≥ 5 nem teljesül.
II. eset: (amikor az abszolútértékben levő szám negatív, azaz < 0)
Tehát 2 - x < 0
2 < x vagy intervallummal x ε ] 2 ; + végtelen [ esetén:
-1 * (2 - x) = 7 - 2x
-2 + x = 7 - 2x / + 2x
3x - 2 = 7 / + 2
3x = 9 / : 3
x = 3 Megoldás, mert benne van az értelmezési tartományban. 2 < 3 teljesül.
Ellenőrzés:
|2 - 5| = 7 - 2 * 5
|-3| = 7 - 10
3 ≠ -3
|2 - 3| = 7 - 2 * 3
|-1| = 7 - 6
1 = 1
|2 - x| = 7 - 2x
Az abszolútérték definíciója szerint nemnegatív szám abszolútértéke mag,a a szám, negatív szám abszolútértéke pedig a szám pozitív ellentettjével (-1-szeresével) egyenlő.
Ezért két esetet kell vizsgálni.
I. eset: (amikor az abszolútértékben levő szám nemnegatív, azaz ≥ 0)
Tehát 2 - x ≥ 0
2 ≥ x vagy intervallummal x ε ] - végtelen ; 2 ] esetén:
2 - x = 7 - 2x / + 2x
2 + x = 7 / - 2
x = 5 Nem megoldás, mert nincs benne az értelmezési tartományban. 2 ≥ 5 nem teljesül.
II. eset: (amikor az abszolútértékben levő szám negatív, azaz < 0)
Tehát 2 - x < 0
2 < x vagy intervallummal x ε ] 2 ; + végtelen [ esetén:
-1 * (2 - x) = 7 - 2x
-2 + x = 7 - 2x / + 2x
3x - 2 = 7 / + 2
3x = 9 / : 3
x = 3 Megoldás, mert benne van az értelmezési tartományban. 2 < 3 teljesül.
Ellenőrzés:
|2 - 5| = 7 - 2 * 5
|-3| = 7 - 10
3 ≠ -3
|2 - 3| = 7 - 2 * 3
|-1| = 7 - 6
1 = 1
0
- Még nem érkezett komment!
 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
b)
1 + log2(2x2 - 3) = 2 * log2(2x - 1)
Értelmezési tartomány: (logaritmus argumentuma csak pozitív szám lehet)
I. 2x2 - 3 > 0
2x2 > 3
x2 > 3/2 = 1,5
x2 = 1,5
x = ± √ 1,5
A másodfokú kifejezés pozitív előjelű, tehát a grafikonja "mosolygós" felfele nyíló parabola lenne, amely az x-tengelyt a -√ 1,5 -ben és a +√ 1,5 -ben metszi.
A másodfukú kifejezés akkor pozitív, ha a grafikonja az x-tengely fölött van, tehát az egyenlőtlenség megoldása:
x < -√ 1,5 vagy x > +√ 1,5 vagy intervallummal: x ε ] - végtelen ; -√ 1,5 [ ∪ ] +√ 1,5 , + végtelen[
II. 2x - 1 > 0
2x > 1
x > 1/2 = 0,5
Az I. és a II. egyenlőtlenségek közös megoldása: x > 0,5
Az egyenlet értelmezési tartománya: x > 0,5
Az egyenlet megoldásánál átalakítjuk az egyenlet mindkét oldalát a logaritmus azonosságainak használatával úgy, hogy az egyenlet mindkét oldalán 1 azonos alapú logaritmus álljon.
log221 + log2(2x2 - 3) =l log2(2x - 1)2
log2 2 * (2x2 - 3) = log2 (2x - 1)2
A log. fgv. szig. mon. miatt
2 * (2x2 - 3) = (2x - 1)2
4x2 - 6 = (2x)2 - 2 * 2x * 1 + 12
4x2 - 6 = 4x2 - 4x + 1 / - 4x2
-6 = -4x + 1 / - 1
-7 = -4x /: (-4)
7/4 = x Megoldás, mert benne van az értelmezési tartományban. 7/4 = 1,75 > 0,5
1 + log2(2x2 - 3) = 2 * log2(2x - 1)
Értelmezési tartomány: (logaritmus argumentuma csak pozitív szám lehet)
I. 2x2 - 3 > 0
2x2 > 3
x2 > 3/2 = 1,5
x2 = 1,5
x = ± √ 1,5
A másodfokú kifejezés pozitív előjelű, tehát a grafikonja "mosolygós" felfele nyíló parabola lenne, amely az x-tengelyt a -√ 1,5 -ben és a +√ 1,5 -ben metszi.
A másodfukú kifejezés akkor pozitív, ha a grafikonja az x-tengely fölött van, tehát az egyenlőtlenség megoldása:
x < -√ 1,5 vagy x > +√ 1,5 vagy intervallummal: x ε ] - végtelen ; -√ 1,5 [ ∪ ] +√ 1,5 , + végtelen[
II. 2x - 1 > 0
2x > 1
x > 1/2 = 0,5
Az I. és a II. egyenlőtlenségek közös megoldása: x > 0,5
Az egyenlet értelmezési tartománya: x > 0,5
Az egyenlet megoldásánál átalakítjuk az egyenlet mindkét oldalát a logaritmus azonosságainak használatával úgy, hogy az egyenlet mindkét oldalán 1 azonos alapú logaritmus álljon.
log221 + log2(2x2 - 3) =l log2(2x - 1)2
log2 2 * (2x2 - 3) = log2 (2x - 1)2
A log. fgv. szig. mon. miatt
2 * (2x2 - 3) = (2x - 1)2
4x2 - 6 = (2x)2 - 2 * 2x * 1 + 12
4x2 - 6 = 4x2 - 4x + 1 / - 4x2
-6 = -4x + 1 / - 1
-7 = -4x /: (-4)
7/4 = x Megoldás, mert benne van az értelmezési tartományban. 7/4 = 1,75 > 0,5
0
- Még nem érkezett komment!