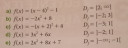Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek SOS
 Kawich
kérdése
Kawich
kérdése
554
"Állapítsd meg a következő függvények szélsőértékhelyeit és szélsőértékeit"
Jelenleg 1 felhasználó nézi ezt a kérdést.
matek
matek
0
Középiskola / Matematika
Válaszok
1 Nagy-Gombás Szilvi
{ Tanár }
megoldása
Nagy-Gombás Szilvi
{ Tanár }
megoldása
Másodfokú függvények grafikonja parabola. A parabolának a "csúcspontjában" van a szésőértéke. Ha a függvény pozitív előjelű, akkor a grafikonja "mosolygós" felfele nyíló parabola, ekkor minimuma van a függvénynek. Ha függvény negatív előjelű, akkor a grafikonja "sírós" lefele nyíló parabola, ekkor maximuma van a függvénynek.
a)
f(x) = (x - 4)2 - 1
Az alapfüggvényt a változótranszformáció miatt az x-tengely mentén eltoljuk 4-gyel pozitív irányba (mindig ellentétesen) és az értéktranszformáció miatt az y-tengely mentén eltoljuk 1-gyel negatív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (4 , -1) koordinátájú pontba került. Mivel a függvény pozitív előjelű, így a parabola "mosolygós" felfele nyíló, tehát a függvénynek minimuma van.
Minimum hely: x = 4
Minimum érték: y = -1 vagy f(x) = -1
b)
f(x) = -2x2 + 8
Nincs változótranszformáció, ezért az alapfüggvényt az x-tengely mentén nem toljuk el, az értéktranszformáció miatt az y-tengely mentén eltoljuk 8-cal pozitív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (0 , 8) koordinátájú pontba került. Mivel a függvény negatív előjelű, így a parabola "sírós" lefele nyíló, tehát a függvénynek maximuma van.
Maximum hely: x = 0
Maximum érték: y = 8 vagy f(x) = 8
c)
f(x) = -(x + 2)2 + 4
Az alapfüggvényt a változótranszformáció miatt az x-tengely mentén eltoljuk 2-vel negatív irányba (mindig ellentétesen) és az értéktranszformáció miatt az y-tengely mentén eltoljuk 4-gyel pozitív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (-2 , 4) koordinátájú pontba került. Mivel a függvény negatív előjelű, így a parabola "sírós" lefele nyíló, tehát a függvénynek maximuma van.
Maximum hely: x = -2
Minimum érték: y = 4 vagy f(x) = 4
d)
f(x) = 3x2 + 6x
Az ábrázoláshoz teljes négyzetté kell alakítani a függvény hozzárendelési utasítását:
f(x) = 3x2 + 6x = 3 * (x2 + 2x) = 3 * [ (x + 1)2 - 12 ] = 3 * [ (x + 1)2 - 1] = 3(x + 1)2 - 3
Tehát:
f(x) = 3(x + 1)2 - 3
Az alapfüggvényt a változótranszformáció miatt az x-tengely mentén eltoljuk 1-gyel negatív irányba (mindig ellentétesen) és az értéktranszformáció miatt az y-tengely mentén eltoljuk 3-mal negatív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (-1 , -3) koordinátájú pontba került. Mivel a függvény pozitív előjelű, így a parabola "mosolygós" felfele nyíló, tehát a függvénynek minimuma van.
Minimum hely: x = -1
Minimum érték: y = -3 vagy f(x) = -3
e)
f(x) = 2x2 + 8x + 7
Az ábrázoláshoz teljes négyzetté kell alakítani a függvény hozzárendelési utasítását:
f(x) = 2x2 + 8x + 7 = 2 * (x2 + 4x) + 7 = 2 * [ (x + 2)2 - 22 ] + 7 = 2 * [ (x + 2)2 - 4] + 7 = 2(x + 2)2 - 8 + 7 = 2(x + 2)2 - 1
Tehát:
f(x) = 2(x + 2)2 - 1
Az alapfüggvényt a változótranszformáció miatt az x-tengely mentén eltoljuk 2-vel negatív irányba (mindig ellentétesen) és az értéktranszformáció miatt az y-tengely mentén eltoljuk 1-gyel negatív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (-2 , -1) koordinátájú pontba került. Mivel a függvény pozitív előjelű, így a parabola "mosolygós" felfele nyíló, tehát a függvénynek minimuma van.
Minimum hely: x = -2
Minimum érték: y = -1 vagy f(x) = -1
a)
f(x) = (x - 4)2 - 1
Az alapfüggvényt a változótranszformáció miatt az x-tengely mentén eltoljuk 4-gyel pozitív irányba (mindig ellentétesen) és az értéktranszformáció miatt az y-tengely mentén eltoljuk 1-gyel negatív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (4 , -1) koordinátájú pontba került. Mivel a függvény pozitív előjelű, így a parabola "mosolygós" felfele nyíló, tehát a függvénynek minimuma van.
Minimum hely: x = 4
Minimum érték: y = -1 vagy f(x) = -1
b)
f(x) = -2x2 + 8
Nincs változótranszformáció, ezért az alapfüggvényt az x-tengely mentén nem toljuk el, az értéktranszformáció miatt az y-tengely mentén eltoljuk 8-cal pozitív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (0 , 8) koordinátájú pontba került. Mivel a függvény negatív előjelű, így a parabola "sírós" lefele nyíló, tehát a függvénynek maximuma van.
Maximum hely: x = 0
Maximum érték: y = 8 vagy f(x) = 8
c)
f(x) = -(x + 2)2 + 4
Az alapfüggvényt a változótranszformáció miatt az x-tengely mentén eltoljuk 2-vel negatív irányba (mindig ellentétesen) és az értéktranszformáció miatt az y-tengely mentén eltoljuk 4-gyel pozitív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (-2 , 4) koordinátájú pontba került. Mivel a függvény negatív előjelű, így a parabola "sírós" lefele nyíló, tehát a függvénynek maximuma van.
Maximum hely: x = -2
Minimum érték: y = 4 vagy f(x) = 4
d)
f(x) = 3x2 + 6x
Az ábrázoláshoz teljes négyzetté kell alakítani a függvény hozzárendelési utasítását:
f(x) = 3x2 + 6x = 3 * (x2 + 2x) = 3 * [ (x + 1)2 - 12 ] = 3 * [ (x + 1)2 - 1] = 3(x + 1)2 - 3
Tehát:
f(x) = 3(x + 1)2 - 3
Az alapfüggvényt a változótranszformáció miatt az x-tengely mentén eltoljuk 1-gyel negatív irányba (mindig ellentétesen) és az értéktranszformáció miatt az y-tengely mentén eltoljuk 3-mal negatív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (-1 , -3) koordinátájú pontba került. Mivel a függvény pozitív előjelű, így a parabola "mosolygós" felfele nyíló, tehát a függvénynek minimuma van.
Minimum hely: x = -1
Minimum érték: y = -3 vagy f(x) = -3
e)
f(x) = 2x2 + 8x + 7
Az ábrázoláshoz teljes négyzetté kell alakítani a függvény hozzárendelési utasítását:
f(x) = 2x2 + 8x + 7 = 2 * (x2 + 4x) + 7 = 2 * [ (x + 2)2 - 22 ] + 7 = 2 * [ (x + 2)2 - 4] + 7 = 2(x + 2)2 - 8 + 7 = 2(x + 2)2 - 1
Tehát:
f(x) = 2(x + 2)2 - 1
Az alapfüggvényt a változótranszformáció miatt az x-tengely mentén eltoljuk 2-vel negatív irányba (mindig ellentétesen) és az értéktranszformáció miatt az y-tengely mentén eltoljuk 1-gyel negatív irányba (mindig megegyező irányba). Így a parabola csúcspontja a (-2 , -1) koordinátájú pontba került. Mivel a függvény pozitív előjelű, így a parabola "mosolygós" felfele nyíló, tehát a függvénynek minimuma van.
Minimum hely: x = -2
Minimum érték: y = -1 vagy f(x) = -1
1
- Még nem érkezett komment!