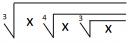Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Gyökös feladatok
 Mark14
kérdése
Mark14
kérdése
1573
1. Egyetlen gyökjellel kell leírni!
³√x⁴√x³√x
2.Gyöktelenítsd az alábbi törtek nevezőit!
a, 10
_____
3√5
b, 2
______
3√2+4
3.Gyökjel alól való kiemeléssel hozd egyszerűbb alakba!
a, √75-3√12+2√27
b, ³√81a⁴-³√8a⁸
³√x⁴√x³√x
2.Gyöktelenítsd az alábbi törtek nevezőit!
a, 10
_____
3√5
b, 2
______
3√2+4
3.Gyökjel alól való kiemeléssel hozd egyszerűbb alakba!
a, √75-3√12+2√27
b, ³√81a⁴-³√8a⁸
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 Rantnad
{
Rantnad
{  }
válasza
}
válasza
1. Ha jól sejtem, akkor a csatolmányban szereplő feladat akar lenni a feladat. Ha igen, akkor kezdjük a kikötéssel; páros gyök alatt nem állhat negatív szám, ezért:
x*³√x≥0, egy kéttényezős szorzat értéke akkor pozitív, hogyha a tényezők előjelei megegyeznek; ha x>0, akkor ³√x>0, tehát mindkettő pozitív, ez jó, hogyha x=0, akkor ³√x=0, tehát a szorzat értéke 0, ez is lehet, ha pedig x<0, akkor ³√x<0, tehát mindkettő negatív, így szorzatuk pozitív lesz, tehát a kifejezés értelmezési tartománya a valós számok halmaza.
Azt kell felhasználnunk, hogy k√a * k√b =k√ a*b , vagyis ha van két, azonos gyökszám alatt álló számunk, akkor azok szorzatát úgy is megkaphatjuk, hogy a számok gyökét vesszük.
A legbelső gyökjel alatt így járunk el: x*³√x=³√ x³ *³√x=³√ x³*x , itt pedig a hatványozás azonosságát használjuk: ak*an=ak+n, vagyis azonos alapú hatványok szorzásánál az alapot a kitevők összegére emelhetjük, így lesz =³√ x3+1 =³√ x⁴ .
A következő lépésben a ⁴√(³√ x⁴ )-nel kell foglalkoznunk, innen két lehetőség is adódik; az egyik, hogy k√ ⁿ√a =n*k√a, vagyis ha egy számból többször akarunk gyököt vonni, akkor egy lépésben úgy is megtehetjük, hogy a gyökszámokat összeszorozzuk, és azzal a számmal vonunk gyököt, esetünkben ¹²√(x⁴), a másik lehetőség, hogy a gyökök tetszőlegesen felcserélhetőek, például így: ³√ ⁴√(x⁴) , itt pedig már el tudjuk végezni a gyökvonást definíció szerint, így ³√|x| marad. Értelemszerűen az előző alak is átvariálható ilyen módon, és hasonló módon megy, mint a felcseréléssel.
Tehát a feladat, amit meg kell még oldanunk: ³√ x*³√|x| , innen esetszétválasztással kell továbbmennünk; ha x≥0, akkor minden gond nélkül elhagyható az ||, így ³√ x*³√x kifejezést kell még egyszerűbb alakban felírnunk, ez ugyanazon az elven megy, ahogy már egyszer leírtam, a végeredmény ⁹√(x⁴).
Ha x<0, akkor x abszolutértéke annak ellentettje lesz, vagy -x, tehát a ³√ x*³√(-x) kifejezést kell átalakítanunk, ennek végeredménye ⁹√(-(x)⁴), a páratlan gyökvonás tulajdonságai miatt a negatív előjel kihozható előre, így a -⁹√(x⁴) alakot kapjuk végeredményül.
2a) Egyszerűen bővítjük (tehát a számlálót és a nevezőt is szorozzuk) √5-tel, ekkor (10*√5)/(3*√5*√5) = (10*√5)/(3*5), itt észrevesszük, hogy 5-tel tudunk egyszerűsíteni, így (2*√5)/3 lesz a végleges alak.
2b) Itt kihasználjuk azt az azonosságot, hogy (a+b)*(a-b)=a²-b², így ha a törtet (3*√2-4)-gyel bővítjük, akkor a nevezőben (3*√2+4)*(3*√2-4)=(3*√2)²-4²=9*2-16=18-16=2 lesz, tehát a tört:
(2*(3*√2-4))/2, 2-vel egyszerűsítve 3*√2-4 marad.
3a) Ehhez az k√a * k√b =k√ a*b azonosságot kell használni, csak visszafelé:
√ 75 =√ 25*3 =√ 25 *√3=5*√3
√ 12 =√ 4*3 =√4*√3=2*√3
√ 27 =√ 9*3 =√9*√3=3*√3, tehát a feladatból ez lesz:
5*√3-3*3*√3+2*2*√3 = 5*√3-9*√3+4*√3, ha tanultál már egyenletmegoldást, akkor az összevonás pont úgy megy, mint például 2x+3x=5x esetén, tehát 5-9+4=0, tehát 0*√3 az eredmény, ami 0. Ha tanultál kiemelést, akkor kiemeljük a √3-at, ekkor √3*(5-9+4)=√3*0=0 az eredmény. Ha ezek közül egyiket sem tanultad, akkor használhatjuk a szorzat definícióját: a*b=b+b+b+...+b, ahol a jobb oldalon 'a' darab 'b'-t adtunk össze, ezt használva:
5*√3=√3+√3+√3+√3+√3
9*√3=√3+√3+√3+√3+√3+√3+√3+√3+√3
4*√3=√3+√3+√3+√3, tehát:
√3+√3+√3+√3+√3-(√3+√3+√3+√3+√3+√3+√3+√3+√3)+√3+√3+√3+√3=
=√3+√3+√3+√3+√3-√3-√3-√3-√3-√3-√3-√3-√3-√3+√3+√3+√3+√3, ezeket összeházasítod, a párok kiejtik egymást (mivel √3-√3=0), így a végére 0 marad.
2b) Itt hogyan vannak gyökjel alatt?
x*³√x≥0, egy kéttényezős szorzat értéke akkor pozitív, hogyha a tényezők előjelei megegyeznek; ha x>0, akkor ³√x>0, tehát mindkettő pozitív, ez jó, hogyha x=0, akkor ³√x=0, tehát a szorzat értéke 0, ez is lehet, ha pedig x<0, akkor ³√x<0, tehát mindkettő negatív, így szorzatuk pozitív lesz, tehát a kifejezés értelmezési tartománya a valós számok halmaza.
Azt kell felhasználnunk, hogy k√a * k√b =k√ a*b , vagyis ha van két, azonos gyökszám alatt álló számunk, akkor azok szorzatát úgy is megkaphatjuk, hogy a számok gyökét vesszük.
A legbelső gyökjel alatt így járunk el: x*³√x=³√ x³ *³√x=³√ x³*x , itt pedig a hatványozás azonosságát használjuk: ak*an=ak+n, vagyis azonos alapú hatványok szorzásánál az alapot a kitevők összegére emelhetjük, így lesz =³√ x3+1 =³√ x⁴ .
A következő lépésben a ⁴√(³√ x⁴ )-nel kell foglalkoznunk, innen két lehetőség is adódik; az egyik, hogy k√ ⁿ√a =n*k√a, vagyis ha egy számból többször akarunk gyököt vonni, akkor egy lépésben úgy is megtehetjük, hogy a gyökszámokat összeszorozzuk, és azzal a számmal vonunk gyököt, esetünkben ¹²√(x⁴), a másik lehetőség, hogy a gyökök tetszőlegesen felcserélhetőek, például így: ³√ ⁴√(x⁴) , itt pedig már el tudjuk végezni a gyökvonást definíció szerint, így ³√|x| marad. Értelemszerűen az előző alak is átvariálható ilyen módon, és hasonló módon megy, mint a felcseréléssel.
Tehát a feladat, amit meg kell még oldanunk: ³√ x*³√|x| , innen esetszétválasztással kell továbbmennünk; ha x≥0, akkor minden gond nélkül elhagyható az ||, így ³√ x*³√x kifejezést kell még egyszerűbb alakban felírnunk, ez ugyanazon az elven megy, ahogy már egyszer leírtam, a végeredmény ⁹√(x⁴).
Ha x<0, akkor x abszolutértéke annak ellentettje lesz, vagy -x, tehát a ³√ x*³√(-x) kifejezést kell átalakítanunk, ennek végeredménye ⁹√(-(x)⁴), a páratlan gyökvonás tulajdonságai miatt a negatív előjel kihozható előre, így a -⁹√(x⁴) alakot kapjuk végeredményül.
2a) Egyszerűen bővítjük (tehát a számlálót és a nevezőt is szorozzuk) √5-tel, ekkor (10*√5)/(3*√5*√5) = (10*√5)/(3*5), itt észrevesszük, hogy 5-tel tudunk egyszerűsíteni, így (2*√5)/3 lesz a végleges alak.
2b) Itt kihasználjuk azt az azonosságot, hogy (a+b)*(a-b)=a²-b², így ha a törtet (3*√2-4)-gyel bővítjük, akkor a nevezőben (3*√2+4)*(3*√2-4)=(3*√2)²-4²=9*2-16=18-16=2 lesz, tehát a tört:
(2*(3*√2-4))/2, 2-vel egyszerűsítve 3*√2-4 marad.
3a) Ehhez az k√a * k√b =k√ a*b azonosságot kell használni, csak visszafelé:
√ 75 =√ 25*3 =√ 25 *√3=5*√3
√ 12 =√ 4*3 =√4*√3=2*√3
√ 27 =√ 9*3 =√9*√3=3*√3, tehát a feladatból ez lesz:
5*√3-3*3*√3+2*2*√3 = 5*√3-9*√3+4*√3, ha tanultál már egyenletmegoldást, akkor az összevonás pont úgy megy, mint például 2x+3x=5x esetén, tehát 5-9+4=0, tehát 0*√3 az eredmény, ami 0. Ha tanultál kiemelést, akkor kiemeljük a √3-at, ekkor √3*(5-9+4)=√3*0=0 az eredmény. Ha ezek közül egyiket sem tanultad, akkor használhatjuk a szorzat definícióját: a*b=b+b+b+...+b, ahol a jobb oldalon 'a' darab 'b'-t adtunk össze, ezt használva:
5*√3=√3+√3+√3+√3+√3
9*√3=√3+√3+√3+√3+√3+√3+√3+√3+√3
4*√3=√3+√3+√3+√3, tehát:
√3+√3+√3+√3+√3-(√3+√3+√3+√3+√3+√3+√3+√3+√3)+√3+√3+√3+√3=
=√3+√3+√3+√3+√3-√3-√3-√3-√3-√3-√3-√3-√3-√3+√3+√3+√3+√3, ezeket összeházasítod, a párok kiejtik egymást (mivel √3-√3=0), így a végére 0 marad.
2b) Itt hogyan vannak gyökjel alatt?
1
- Még nem érkezett komment!