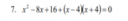Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valaki tudna segíteni?
 ju.david
kérdése
ju.david
kérdése
459
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 Nagy-Gombás Szilvi
{ Tanár }
megoldása
Nagy-Gombás Szilvi
{ Tanár }
megoldása
1. feladat:
(4x - 3) * (x2 + 2x + 1) = 0
Az x2 + 2x + 1 egy teljes négyzet, x2 + 2x + 1 = ( x + 1)2 alakba írható át.
A megoldandó egyenlet:
(4x - 3) * (x + 1)2 = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. 4x - 3 = 0
4x = 3
x1 = 3/4 = 0,75
II. ( x + 1)2 = 0
x + 1 = 0
x2 = -1
2. feladat:
x2 - 8x = 0
Hiányos másodfokú egyenlet, az x kiemelésével szorzattá alakítható.
x * ( x - 8) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x1 = 0
II. x - 8 = 0
x2 = 8
3. feladat:
x3 - 4x = 0
Hiányos harmadfokú egyenlet, az x kiemelésével szorzattá alakítható.
x * (x2 - 4) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x1 = 0
II. x2 - 4 = 0
Hiányos másodfokú egyenlet, az a2 - b2 = (a - b) * (a + b) azonosság alkalmazásával szorzattá alakítható.
x2 - 4 = 0
x2 - 22 = 0
(x - 2) * (x + 2) = 0
II. a) x - 2 = 0
x2 = 2
II. b) x + 2 = 0
x3 = -2
4. feladat:
x3 + 6x2 + 9x = 0
Hiányos harmadfokú egyenlet, az x kiemelésével szorzattá alakítható.
x * (x2 + 6x + 9) = 0
x2 + 6x + 9 egy teljes négyzet, x2 + 6x + 9 = (x + 3)2 alakba írható át.
Tehát:
x * (x + 3)2 = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x1 = 0
II. (x + 3)2 = 0
x + 3 = 0
x2 = -3
5. feladat:
x2 - 3x + 2x - 6 = 0
Másodfokú egyenlet, ami csoportos kiemeléssel szorzattá alakítható.
x * (x - 3) + 2 * (x - 3) = 0
(x - 3) * (x + 2) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x - 3 = 0
x1 = 3
II. x + 2 = 0
x2 = -2
6. feladat: Elírták, valamelyik előjel téves.
12x + 4x2 + 2x + 6 = 0
Másodfokú egyenlet, ami csoportos kiemeléssel szorzattá alakítható.
4x * (3 + x) + 2 * (x + 3) = 0 (3 + x = x + 3)
(x + 3) * (4x + 2) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x + 3 = 0
x1 = -3
II. 4x + 2 = 0
4x = -2
x2 = -2/4 = -1/2 = -0,5
Vagy:
12x - 4x2 + 2x - 6 = 0
Másodfokú egyenlet, ami csoportos kiemeléssel szorzattá alakítható.
4x * (3 - x) + 2 * (x - 3) = 0 (3 - x = -(x - 3) )
(x - 3) * (-4x + 2) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x - 3 = 0
x1 = 3
II. -4x + 2 = 0
2 = 4x
x2 = 2/4 = 1/2 = 0,5
Vagy:
12x - 4x2 - 2x + 6 = 0
Másodfokú egyenlet, ami csoportos kiemeléssel szorzattá alakítható.
4x * (3 - x) - 2 * (x - 3) = 0 (3 - x = -(x - 3))
(x - 3) * (-4x - 2) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x - 3 = 0
x1 = 3
II. -4x - 2 = 0
-2 = 4x
x2 = -2/4 = -1/2 = -0,5
(4x - 3) * (x2 + 2x + 1) = 0
Az x2 + 2x + 1 egy teljes négyzet, x2 + 2x + 1 = ( x + 1)2 alakba írható át.
A megoldandó egyenlet:
(4x - 3) * (x + 1)2 = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. 4x - 3 = 0
4x = 3
x1 = 3/4 = 0,75
II. ( x + 1)2 = 0
x + 1 = 0
x2 = -1
2. feladat:
x2 - 8x = 0
Hiányos másodfokú egyenlet, az x kiemelésével szorzattá alakítható.
x * ( x - 8) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x1 = 0
II. x - 8 = 0
x2 = 8
3. feladat:
x3 - 4x = 0
Hiányos harmadfokú egyenlet, az x kiemelésével szorzattá alakítható.
x * (x2 - 4) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x1 = 0
II. x2 - 4 = 0
Hiányos másodfokú egyenlet, az a2 - b2 = (a - b) * (a + b) azonosság alkalmazásával szorzattá alakítható.
x2 - 4 = 0
x2 - 22 = 0
(x - 2) * (x + 2) = 0
II. a) x - 2 = 0
x2 = 2
II. b) x + 2 = 0
x3 = -2
4. feladat:
x3 + 6x2 + 9x = 0
Hiányos harmadfokú egyenlet, az x kiemelésével szorzattá alakítható.
x * (x2 + 6x + 9) = 0
x2 + 6x + 9 egy teljes négyzet, x2 + 6x + 9 = (x + 3)2 alakba írható át.
Tehát:
x * (x + 3)2 = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x1 = 0
II. (x + 3)2 = 0
x + 3 = 0
x2 = -3
5. feladat:
x2 - 3x + 2x - 6 = 0
Másodfokú egyenlet, ami csoportos kiemeléssel szorzattá alakítható.
x * (x - 3) + 2 * (x - 3) = 0
(x - 3) * (x + 2) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x - 3 = 0
x1 = 3
II. x + 2 = 0
x2 = -2
6. feladat: Elírták, valamelyik előjel téves.
12x + 4x2 + 2x + 6 = 0
Másodfokú egyenlet, ami csoportos kiemeléssel szorzattá alakítható.
4x * (3 + x) + 2 * (x + 3) = 0 (3 + x = x + 3)
(x + 3) * (4x + 2) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x + 3 = 0
x1 = -3
II. 4x + 2 = 0
4x = -2
x2 = -2/4 = -1/2 = -0,5
Vagy:
12x - 4x2 + 2x - 6 = 0
Másodfokú egyenlet, ami csoportos kiemeléssel szorzattá alakítható.
4x * (3 - x) + 2 * (x - 3) = 0 (3 - x = -(x - 3) )
(x - 3) * (-4x + 2) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x - 3 = 0
x1 = 3
II. -4x + 2 = 0
2 = 4x
x2 = 2/4 = 1/2 = 0,5
Vagy:
12x - 4x2 - 2x + 6 = 0
Másodfokú egyenlet, ami csoportos kiemeléssel szorzattá alakítható.
4x * (3 - x) - 2 * (x - 3) = 0 (3 - x = -(x - 3))
(x - 3) * (-4x - 2) = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0, tehát:
I. x - 3 = 0
x1 = 3
II. -4x - 2 = 0
-2 = 4x
x2 = -2/4 = -1/2 = -0,5
0
- Még nem érkezett komment!
 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
7. feladat:
x2 - 8x + 16 + (x - 4) * (x + 4) = 0
Az x2 - 8x + 16 egy teljes négyzet, x2 - 8x + 16 = (x - 4)2 alakba írható át.
A megoldandó egyenlet tehát:
(x - 4)2 + (x - 4) * (x + 4) = 0
Másodfokú egyenlet, amely kiemeléssel szorzattá alakítható.
(x - 4) * [(x - 4) + (x + 4)] = 0
(x - 4) * (x - 4 + x + 4) = 0
(x - 4) * 2x = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0 , azaz:
I. x - 4 = 0
x1 = 4
II. 2x = 0
x2 = 0
x2 - 8x + 16 + (x - 4) * (x + 4) = 0
Az x2 - 8x + 16 egy teljes négyzet, x2 - 8x + 16 = (x - 4)2 alakba írható át.
A megoldandó egyenlet tehát:
(x - 4)2 + (x - 4) * (x + 4) = 0
Másodfokú egyenlet, amely kiemeléssel szorzattá alakítható.
(x - 4) * [(x - 4) + (x + 4)] = 0
(x - 4) * (x - 4 + x + 4) = 0
(x - 4) * 2x = 0
Egy szorzat akkor egyenlő 0-val, ha valamelyik szorzótényezője 0 , azaz:
I. x - 4 = 0
x1 = 4
II. 2x = 0
x2 = 0
0
- Még nem érkezett komment!