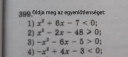Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Segítség!!!!
 weinrauchmelinda
kérdése
weinrauchmelinda
kérdése
376
Segítség!!!!!!
Jelenleg 1 felhasználó nézi ezt a kérdést.
Sos!!!!
Sos!!!!
0
Általános iskola / Matematika
Válaszok
1 Nagy-Gombás Szilvi
{ Tanár }
megoldása
Nagy-Gombás Szilvi
{ Tanár }
megoldása
399. feladat:
1)
x2 + 6x - 7 < 0 A másodfokú kifejezés kisebb 0-nál, tehát negatív.
Behelyettesítünk a megoldóképletbe:
D = 62 - 4 * 1 * (-7) = 36 + 28 = 64 = 82
x1,2 = (-6 ± 8) / 2
x1 = (-6 + 8) / 2 = 2 / 2 = 1
x2 = (-6 - 8) / 2 = -14 / 2 = -7
Tehát, ha a másodfokú kifejezést függvényként (parabola) ábrázoljuk, akkor a függvény zérushelyei (ahol a függvény az x tengelyt metszi) az 1 és a -7.
Mivel az x2 pozitív, ezért a parabola "mosolygós" felfele nyíló és az x tengelyt az 1-ben és a -7-ben metszi.
Azt keressük, hogy a függvény hol negatív. A függvény ott negatív, ahol a függvény grafikonja az x tengely alatt van.
Ez a függvény a -7 és az 1 között van a tengely alatt, vagyis az egyenlőtlenség megoldása: -7< x < 1, vagy intervallummal:
x ε ]-7 ; 1[.
2)
x2 - 2x - 48 ≥ 0 A másodfokú kifejezés nagyobb vagy egyenlő 0-nál, tehát nemnegatív (pozitív vagy 0).
Behelyettesítünk a megoldóképletbe:
D = (-2)2 - 4 * 1 * (-48) = 4 + 192 = 196 = 142
x1,2 = (2 ± 14) / 2
x1 = (2 + 14) / 2 = 16 / 2 = 8
x2 = (2 - 14) / 2 = -12 / 2 = -6
Tehát, ha a másodfokú kifejezést függvényként (parabola) ábrázoljuk, akkor a függvény zérushelyei (ahol a függvény az x tengelyt metszi) a 8 és a -6.
Mivel az x2 pozitív, ezért a parabola "mosolygós" felfele nyíló és az x tengelyt a 8-ban és a -6-ban metszi.
Azt keressük, hogy a függvény hol pozitív. A függvény ott pozitív, ahol a függvény grafikonja az x tengely felett van.
Ez a függvény a -6 előtt és a 8 után van a tengely felett, vagyis az egyenlőtlenség megoldása: x ≤ -6 vagy x ≥ 8, vagy intervallummal: x ε ]-végtelen ; -6] ∪ [8 ; végtelen[. (A zérushelyeknél zárt az intervallum, mert az egyenlőség is megengedett.)
3)
-x2 - 6x - 5 > 0 A másodfokú kifejezés nagyobb 0-nál, tehát pozitív.
Behelyettesítünk a megoldóképletbe:
D = 62 - 4 * (-1) * (-5) = 36 - 20 = 16 = 42
x1,2 = (-6 ± 4) / (-2)
x1 = (-6 + 4) / (-2) = -2 / (-2) = 1
x2 = (-6 - 4) / 2 = -10 / (-2) = 5
Tehát, ha a másodfokú kifejezést függvényként (parabola) ábrázoljuk, akkor a függvény zérushelyei (ahol a függvény az x tengelyt metszi) az 1 és az 5.
Mivel az x2 negatív, ezért a parabola "sírós" lefele nyíló és az x tengelyt az 1-ben és az 5-ben metszi.
Azt keressük, hogy a függvény hol pozitív. A függvény ott pozitív, ahol a függvény grafikonja az x tengely felett van.
Ez a függvény az 1 és az 5 között van a tengely felett, vagyis az egyenlőtlenség megoldása: 1< x < 5, vagy intervallummal:
x ε ]1 ; 5[.
4)
-x2 + 4x - 3 < 0 A másodfokú kifejezés kisebb 0-nál, tehát negatív.
Behelyettesítünk a megoldóképletbe:
D = 42 - 4 * (-1) * (-3) = 16 - 12 = 4 = 22
x1,2 = (-4 ± 2) / (-2)
x1 = (-4 + 2) / (-2) = -2 / (-2) = 1
x2 = (-4 - 2) / (-2) = -6 / (-2) = 3
Tehát, ha a másodfokú kifejezést függvényként (parabola) ábrázoljuk, akkor a függvény zérushelyei (ahol a függvény az x tengelyt metszi) az 1 és a 3.
Mivel az x2 negatív, ezért a parabola "sírós" lefele nyíló és az x tengelyt az 1-ben és a 3-ban metszi.
Azt keressük, hogy a függvény hol negatív. A függvény ott negatív, ahol a függvény grafikonja az x tengely alatt van.
Ez a függvény az 1 előtt és a 3 után van a tengely alatt, vagyis az egyenlőtlenség megoldása: x < 1 vagy x > 3, vagy intervallummal: x ε ]-végtelen ; 1[ ∪ ]3 ; végtelen[.
1)
x2 + 6x - 7 < 0 A másodfokú kifejezés kisebb 0-nál, tehát negatív.
Behelyettesítünk a megoldóképletbe:
D = 62 - 4 * 1 * (-7) = 36 + 28 = 64 = 82
x1,2 = (-6 ± 8) / 2
x1 = (-6 + 8) / 2 = 2 / 2 = 1
x2 = (-6 - 8) / 2 = -14 / 2 = -7
Tehát, ha a másodfokú kifejezést függvényként (parabola) ábrázoljuk, akkor a függvény zérushelyei (ahol a függvény az x tengelyt metszi) az 1 és a -7.
Mivel az x2 pozitív, ezért a parabola "mosolygós" felfele nyíló és az x tengelyt az 1-ben és a -7-ben metszi.
Azt keressük, hogy a függvény hol negatív. A függvény ott negatív, ahol a függvény grafikonja az x tengely alatt van.
Ez a függvény a -7 és az 1 között van a tengely alatt, vagyis az egyenlőtlenség megoldása: -7< x < 1, vagy intervallummal:
x ε ]-7 ; 1[.
2)
x2 - 2x - 48 ≥ 0 A másodfokú kifejezés nagyobb vagy egyenlő 0-nál, tehát nemnegatív (pozitív vagy 0).
Behelyettesítünk a megoldóképletbe:
D = (-2)2 - 4 * 1 * (-48) = 4 + 192 = 196 = 142
x1,2 = (2 ± 14) / 2
x1 = (2 + 14) / 2 = 16 / 2 = 8
x2 = (2 - 14) / 2 = -12 / 2 = -6
Tehát, ha a másodfokú kifejezést függvényként (parabola) ábrázoljuk, akkor a függvény zérushelyei (ahol a függvény az x tengelyt metszi) a 8 és a -6.
Mivel az x2 pozitív, ezért a parabola "mosolygós" felfele nyíló és az x tengelyt a 8-ban és a -6-ban metszi.
Azt keressük, hogy a függvény hol pozitív. A függvény ott pozitív, ahol a függvény grafikonja az x tengely felett van.
Ez a függvény a -6 előtt és a 8 után van a tengely felett, vagyis az egyenlőtlenség megoldása: x ≤ -6 vagy x ≥ 8, vagy intervallummal: x ε ]-végtelen ; -6] ∪ [8 ; végtelen[. (A zérushelyeknél zárt az intervallum, mert az egyenlőség is megengedett.)
3)
-x2 - 6x - 5 > 0 A másodfokú kifejezés nagyobb 0-nál, tehát pozitív.
Behelyettesítünk a megoldóképletbe:
D = 62 - 4 * (-1) * (-5) = 36 - 20 = 16 = 42
x1,2 = (-6 ± 4) / (-2)
x1 = (-6 + 4) / (-2) = -2 / (-2) = 1
x2 = (-6 - 4) / 2 = -10 / (-2) = 5
Tehát, ha a másodfokú kifejezést függvényként (parabola) ábrázoljuk, akkor a függvény zérushelyei (ahol a függvény az x tengelyt metszi) az 1 és az 5.
Mivel az x2 negatív, ezért a parabola "sírós" lefele nyíló és az x tengelyt az 1-ben és az 5-ben metszi.
Azt keressük, hogy a függvény hol pozitív. A függvény ott pozitív, ahol a függvény grafikonja az x tengely felett van.
Ez a függvény az 1 és az 5 között van a tengely felett, vagyis az egyenlőtlenség megoldása: 1< x < 5, vagy intervallummal:
x ε ]1 ; 5[.
4)
-x2 + 4x - 3 < 0 A másodfokú kifejezés kisebb 0-nál, tehát negatív.
Behelyettesítünk a megoldóképletbe:
D = 42 - 4 * (-1) * (-3) = 16 - 12 = 4 = 22
x1,2 = (-4 ± 2) / (-2)
x1 = (-4 + 2) / (-2) = -2 / (-2) = 1
x2 = (-4 - 2) / (-2) = -6 / (-2) = 3
Tehát, ha a másodfokú kifejezést függvényként (parabola) ábrázoljuk, akkor a függvény zérushelyei (ahol a függvény az x tengelyt metszi) az 1 és a 3.
Mivel az x2 negatív, ezért a parabola "sírós" lefele nyíló és az x tengelyt az 1-ben és a 3-ban metszi.
Azt keressük, hogy a függvény hol negatív. A függvény ott negatív, ahol a függvény grafikonja az x tengely alatt van.
Ez a függvény az 1 előtt és a 3 után van a tengely alatt, vagyis az egyenlőtlenség megoldása: x < 1 vagy x > 3, vagy intervallummal: x ε ]-végtelen ; 1[ ∪ ]3 ; végtelen[.
1
-
weinrauchmelinda: Köszönöm! 5 éve 0
-
weinrauchmelinda: Köszönöm! 5 éve 0