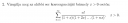Toplista
- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Sorok konvergenciája
astaw41
kérdése
510
Sorok konvergenciája
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1
bongolo
{ 
}
megoldása
Hányadoskritériumot tudsz használni:
an+1/an = (n+1)! / n! ·(1+x)(1+2x)...(1+nx) / (1+x)(1+2x)...(1+(n+1)x)
= (n+1) / (1 + (n+1)x)
A többi tényező kiejtette egymást.
= 1 / (1/(n+1) + x)
aminek a határértéke 1/x, annak kellene 1-nél kisebbnek lennie.
Vagyis x>1 esetén konvergens, x<1-nél divergens.
x=1-re külön kell megnézni:
Ekkor a szumma ilyenekre megy:
n! / 2·3·...(n+1)
ami 1/(n+1)
Ez 0-hoz tart, tehát a szükséges feltétel teljesül, de ez lesz a szumma:
1/2 + 1/3 + 1/4 + ... a végtelenségig
Azt pedig tudjuk, hogy szumma 1/n divergens.
an+1/an = (n+1)! / n! ·(1+x)(1+2x)...(1+nx) / (1+x)(1+2x)...(1+(n+1)x)
= (n+1) / (1 + (n+1)x)
A többi tényező kiejtette egymást.
= 1 / (1/(n+1) + x)
aminek a határértéke 1/x, annak kellene 1-nél kisebbnek lennie.
Vagyis x>1 esetén konvergens, x<1-nél divergens.
x=1-re külön kell megnézni:
Ekkor a szumma ilyenekre megy:
n! / 2·3·...(n+1)
ami 1/(n+1)
Ez 0-hoz tart, tehát a szükséges feltétel teljesül, de ez lesz a szumma:
1/2 + 1/3 + 1/4 + ... a végtelenségig
Azt pedig tudjuk, hogy szumma 1/n divergens.
Módosítva: 9 éve
1
- Még nem érkezett komment!