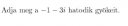Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Adja meg -1-3i hatodik gyökeit(számológép nélkül)
 astaw41
kérdése
astaw41
kérdése
500
Adja meg -1-3i hatodik gyökeit(számológép nélkül)
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 bongolo
{
bongolo
{  }
megoldása
}
megoldása
-1-3i hossza: r = √(1²+3²) = √10
Szöge θ = arc tg ... kicsit trükkös, mert ha felrajzolod a komplex síkra a számot, látod, hogy 180°-nál több kell legyen a szöge, Az arc tg csak ±90°-ig működik. Az arc tg 3 megadja az 1+3i szögét, nekünk éppen π-vel több kell:
θ = π + arc tg 3
Szóval z = r·(cos θ + i·sin θ)
Ennek a hatodik gyökei:
⁶√ z = ⁶√r·(cos((θ+k·2π)/6) + i·sin((θ+k·2π)/6))
ahol k=0,1,2,3,4,5
Pontosabban nem lehet megadni, mert sem √10, sem arc tg 3 nem adható meg számológép nélkül. Szóval vagy csak ez a fenti r-et és θ-t tartalmazó sor a megoldás, vagy ki kell írnod, amíg lehet, de abból ilyen durvák jönnek ki:
z₁ = ¹²√10 · ( cos((π+arc tg3)/6) + i·sin((π+arc tg3)/6) )
z₂ = ¹²√10 · ( cos((3π+arc tg3)/6) + i·sin((3π+arc tg3)/6) )
stb.
z₆ = ¹²√10 · ( cos((11π+arc tg3)/6) + i·sin((11π+arc tg3)/6) )
Szöge θ = arc tg ... kicsit trükkös, mert ha felrajzolod a komplex síkra a számot, látod, hogy 180°-nál több kell legyen a szöge, Az arc tg csak ±90°-ig működik. Az arc tg 3 megadja az 1+3i szögét, nekünk éppen π-vel több kell:
θ = π + arc tg 3
Szóval z = r·(cos θ + i·sin θ)
Ennek a hatodik gyökei:
⁶√ z = ⁶√r·(cos((θ+k·2π)/6) + i·sin((θ+k·2π)/6))
ahol k=0,1,2,3,4,5
Pontosabban nem lehet megadni, mert sem √10, sem arc tg 3 nem adható meg számológép nélkül. Szóval vagy csak ez a fenti r-et és θ-t tartalmazó sor a megoldás, vagy ki kell írnod, amíg lehet, de abból ilyen durvák jönnek ki:
z₁ = ¹²√10 · ( cos((π+arc tg3)/6) + i·sin((π+arc tg3)/6) )
z₂ = ¹²√10 · ( cos((3π+arc tg3)/6) + i·sin((3π+arc tg3)/6) )
stb.
z₆ = ¹²√10 · ( cos((11π+arc tg3)/6) + i·sin((11π+arc tg3)/6) )
1
-
astaw41: Ha pl. ábrázolom, és az első síknegyedbe esik akkor marad ugyanaz, ha pedig a másodikba akkor pí-arctg(x), ha a harmadikba esik, akkor pí+arctg, ha a negyedikbe akkor pedig 2pí-arctg. igaz? 8 éve 0
-
bongolo: igen 8 éve 1