Az elméletet itt hallgathatod meg: https://www.youtube.com/watch?v=tLtByppCt7c
A te feladatod megoldása a képen:

a = 16 cm
b = 19 cm
c = 22 cm
A háromszög általános (nem derékszögű), ezért az oldalaira és szögeire a koszinusz-tételt alkalmazhatjuk.
Az a oldallal szemközti szög α, b-vel szemközti β és c-vel szemközti pedig γ.
Felírjuk a koszinusz-tételt az α szögre:
a2 = b2 + c2 - 2 * b * c * cosα
162 = 192 + 222 - 2 * 19 * 22 * cosα
256 = 361 + 484 - 836 * cosα
256 = 845 - 836 * cosα /-845
-589 = -836 * cosα /:(-836)
0,7045 = cosα
45,21⁰ = α

Most már ismerünk egy szöget, a következő szög számolásához használhatjuk a szinusz-tételt (mert van egy "pár", azaz egy oldal és a vele szemközti szög).
Számoljuk ki a β-t.
b / a = sinβ / sinα
19 / 16 = sinβ / sin45,21⁰
1,1875 = sinβ / 0,7096 /*0,7096
0,8427 = sinβ
57,43⁰ = β

Mivel tudjuk, hogy a háromszög belső szögeinek összege 180⁰, így megkapjuk, hogy
γ = 180⁰ - α - β = 180⁰ - 45,21⁰ - 57,43⁰ = 77,36⁰

A háromszög területét kiszámolhatjuk a trigonometrikus területképlettel:
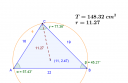
T = (a * b * sinγ) / 2 = (16 * 19 * sin77,36⁰) / 2 =148,32 cm2

A háromszög területét ki lehet számolni az oldalak és a köré írt kör sugarának ismeretében is:
T = (a * b * c) / 4R , ahol a, b, c a háromszög oldalai, R pedig a háromszög köré írható körének a sugara.
Ebbe a területképletbe behelyettesítve kapjuk, hogy
148,32 = (16 * 19 * 22) / 4R
148,32 = 6688 / 4R (egyszerűsítünk a jobb oldalon 4-gyel)
148,32 = 1672 / R
148,32 * R = 1672
R = 11,27 cm a köré írható kör sugara.