Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matematika
 Törölt
kérdése
Törölt
kérdése
1080
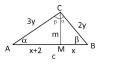
Egy derékszögű háromszög befogóinak aránya 3:2. Az átfogónak a hozzá tartozó magaságvonal által levágott szeletei közül az egyik 2 cm-rel hosszabb a másiknál. Határozzuk meg az átfogó hosszát.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
5 kazah
válasza
kazah
válasza
Ábra
Pitagorasz:
`(2y)^2+(3y)^2=(2x+2)^2`
`13y^2` = `(2x+2)^2`
A hasonló háromszögekben az arányok: (A kis belső háromszögben és a nagyban)
`(2y)/x` = `(2x+2)/(2y)` = `(x+1)/y`
`2y^2` = x(x+1)
`13y^2` = `6.5x(x+1)`
6,5x(x+1) = `(2x+2)^2`
`6,5x^2+6,5x` = `4x^2+8x+4`
`2.5x^2-1.5x-4` = 0
x = `8/5`
Az átfogó a kérdés:
c = 2x+2 = `2*8/5+2` = `26/5` cm
Stimmel az, csak lemaradt egy kettes az elején, javítva.
Pitagorasz:
`(2y)^2+(3y)^2=(2x+2)^2`
`13y^2` = `(2x+2)^2`
A hasonló háromszögekben az arányok: (A kis belső háromszögben és a nagyban)
`(2y)/x` = `(2x+2)/(2y)` = `(x+1)/y`
`2y^2` = x(x+1)
`13y^2` = `6.5x(x+1)`
6,5x(x+1) = `(2x+2)^2`
`6,5x^2+6,5x` = `4x^2+8x+4`
`2.5x^2-1.5x-4` = 0
x = `8/5`
Az átfogó a kérdés:
c = 2x+2 = `2*8/5+2` = `26/5` cm
Stimmel az, csak lemaradt egy kettes az elején, javítva.
Módosítva: 5 éve
0
- Még nem érkezett komment!
 szzs
{ Fortélyos }
megoldása
szzs
{ Fortélyos }
megoldása
Úgy tűnik, ez a jó eredmény: A befogó-tételt felírva:
(2y)2=x (2x+2)
(3y)2=(x+2) (2x+2). Ezt az egyenletrendszert megoldva:
(a második egyenletet osztva az elsővel) x = 1.6.
Ebből: c = 5.2 cm.
(2y)2=x (2x+2)
(3y)2=(x+2) (2x+2). Ezt az egyenletrendszert megoldva:
(a második egyenletet osztva az elsővel) x = 1.6.
Ebből: c = 5.2 cm.
Módosítva: 5 éve
0
- Még nem érkezett komment!
 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
Befogók legyenek : a és b
Ekkor: a : b = 3 : 2
a = 3x
b = 2x
Felírjuk a háromszög oldalaira Pitagorasz-tételét:
a2 + b2 = c2
(3x)2 + (2x)2 = c2
9x2 + 4x2 = c2
13x2 = c2
c = √ 13 x
Az átfogó két szelete legyen: p és q. (p az a melletti szelet, q pedig a b melletti szelet)
Akkor p = q + 2
Felírjuk a-ra a befogó-tételt:
a = √ c * p
a2 = c * p
(3x)2 = √ 13 x *(q + 2)
9x2 = √ 13 x * (q + 2) /: x
9x = √ 13 * (q + 2)
I. 9x = √ 13 * q + 2√ 13
Felírjuk b-re a befogó-tételt:
b = √ c * q
b2 = c * q
(2x)2 = √ 13 x * q
4x2 = √ 13 x * q /: x
II. 4x = √ 13 * q
A II. egyenletet behelyettesítjük I- egyenletbe (√ 13 * q helyére):
9x = 4x + 2√ 13
5x = 2√ 13
x = (2√ 13 ) / 5
Végül x-et visszahelyettesítjük c-be:
c = √ 13 * (2√ 13 /5) = (2 * 13) / 5 = 26/5 = 5,2 cm
A háromszög átfogója 5,2 cm-es.
Ekkor: a : b = 3 : 2
a = 3x
b = 2x
Felírjuk a háromszög oldalaira Pitagorasz-tételét:
a2 + b2 = c2
(3x)2 + (2x)2 = c2
9x2 + 4x2 = c2
13x2 = c2
c = √ 13 x
Az átfogó két szelete legyen: p és q. (p az a melletti szelet, q pedig a b melletti szelet)
Akkor p = q + 2
Felírjuk a-ra a befogó-tételt:
a = √ c * p
a2 = c * p
(3x)2 = √ 13 x *(q + 2)
9x2 = √ 13 x * (q + 2) /: x
9x = √ 13 * (q + 2)
I. 9x = √ 13 * q + 2√ 13
Felírjuk b-re a befogó-tételt:
b = √ c * q
b2 = c * q
(2x)2 = √ 13 x * q
4x2 = √ 13 x * q /: x
II. 4x = √ 13 * q
A II. egyenletet behelyettesítjük I- egyenletbe (√ 13 * q helyére):
9x = 4x + 2√ 13
5x = 2√ 13
x = (2√ 13 ) / 5
Végül x-et visszahelyettesítjük c-be:
c = √ 13 * (2√ 13 /5) = (2 * 13) / 5 = 26/5 = 5,2 cm
A háromszög átfogója 5,2 cm-es.
0
- Még nem érkezett komment!
 DeeDee
válasza
DeeDee
válasza
Kicsit kevesebb kacskaringóval...
Legyen
a, b - a háromszög befogói (a < b)
c - a háromszög átfogója
ca,cb - a befogók vetülete az átfogón
n = a/b - a befogók hányadosa
Feltétel
n = 2/3
cb = ca + 2
Feladat
c = ?
-----------------------------
Befogó tétel szerint
a² = c*ca
b² = c*cb
A két egyenlet hányadosa
(a/b)² = ca/cb
n² = ca/(ca + 2)
Ebből
ca = 2n²/(1 - n²)
******************
Ezzel
cb = ca + 2
cb = 2/(1 - n²)
****************
Ezekkel
c = ca + cb
c = 2(1 + n² )/(1 - n²)
************************
Behelyettesítve
ca = 8/5 = 1,6
cb = 18/5 = 3,6
c = 26/5 = 5,2
================
Legyen
a, b - a háromszög befogói (a < b)
c - a háromszög átfogója
ca,cb - a befogók vetülete az átfogón
n = a/b - a befogók hányadosa
Feltétel
n = 2/3
cb = ca + 2
Feladat
c = ?
-----------------------------
Befogó tétel szerint
a² = c*ca
b² = c*cb
A két egyenlet hányadosa
(a/b)² = ca/cb
n² = ca/(ca + 2)
Ebből
ca = 2n²/(1 - n²)
******************
Ezzel
cb = ca + 2
cb = 2/(1 - n²)
****************
Ezekkel
c = ca + cb
c = 2(1 + n² )/(1 - n²)
************************
Behelyettesítve
ca = 8/5 = 1,6
cb = 18/5 = 3,6
c = 26/5 = 5,2
================
0
- Még nem érkezett komment!