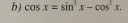Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Tudnátok segíteni?
 Törölt
kérdése
Törölt
kérdése
325
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 velo.gabor
{ Elismert }
megoldása
velo.gabor
{ Elismert }
megoldása
Szia!
cosx=sin2x-cos2x, használd fel a trigonometrikus pitagorasz-tételt a sin2x átalakításához:
sin2x+cos2x=1, amből sin2x=1-cos2x. Ezt behelyettesítve:
cosx=1-cos2x-cos2x /összevonva
cosx=1-2cos2x /-cosx és rendezés
0=-2cos2x-cosx+1 /ami cosx-re nézve másodfokú egyenlet. Legyen cosx=y
0=-2y2-y+1, a=-2, b=-1, c=1 (jöhet a megoldóképlet)
y1,2=(1±√ 1(négyxzet)-4*(-2)*1 )/[2*(-2)]=(1±√ 1+8 )/(-4)=(1±√ 9 )/(-4)=(1±3)/(-4), amiből y1=(1+3)/(-4)=-1, és y2=(1-3)/(-4)=1/2
I. megoldás: ha y=-1, akkor cosx=-1. Ebben az esetben x=180⁰+k*360⁰, vagy radiánban: x=(π/2)+k*2π=π*(1/2+2k) k∈Z
II. megoldás: ha y=1/2, akkor cosx=1/2. Számológéppel visszakeresve x=60⁰, periódus 360⁰, tehát a megoldás:
x=±60⁰+l*360⁰, vagy radiánban x=±π/3+l*2π=π*(±1/3+2l) l∈Z
cosx=sin2x-cos2x, használd fel a trigonometrikus pitagorasz-tételt a sin2x átalakításához:
sin2x+cos2x=1, amből sin2x=1-cos2x. Ezt behelyettesítve:
cosx=1-cos2x-cos2x /összevonva
cosx=1-2cos2x /-cosx és rendezés
0=-2cos2x-cosx+1 /ami cosx-re nézve másodfokú egyenlet. Legyen cosx=y
0=-2y2-y+1, a=-2, b=-1, c=1 (jöhet a megoldóképlet)
y1,2=(1±√ 1(négyxzet)-4*(-2)*1 )/[2*(-2)]=(1±√ 1+8 )/(-4)=(1±√ 9 )/(-4)=(1±3)/(-4), amiből y1=(1+3)/(-4)=-1, és y2=(1-3)/(-4)=1/2
I. megoldás: ha y=-1, akkor cosx=-1. Ebben az esetben x=180⁰+k*360⁰, vagy radiánban: x=(π/2)+k*2π=π*(1/2+2k) k∈Z
II. megoldás: ha y=1/2, akkor cosx=1/2. Számológéppel visszakeresve x=60⁰, periódus 360⁰, tehát a megoldás:
x=±60⁰+l*360⁰, vagy radiánban x=±π/3+l*2π=π*(±1/3+2l) l∈Z
0
- Még nem érkezett komment!