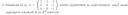Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Lineáris Algebra
 R2D2
kérdése
R2D2
kérdése
320
Az összes kérdés kiemelésre fog kerülni amit ma fel töltöttem , 15 perc elteltével .
Ha lehetséges levezetést is szeretnék és a válaszokat előre is köszönöm!
Ha lehetséges levezetést is szeretnék és a válaszokat előre is köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
A sajátvektorok azok a vektorok, amiket a mátrix (mint transzformáció) nem forgat el, csak megnyújt vagy összenyom. Más szóval a sajátvektorokat a mátrixszal való szorzás önmaguk skalárszorosaivá skálázza, a skálatényezők a sajátértékek. Egyenlettel: `\mathbf{A}\mathbf{v}=lambda \mathbf{v}`. Rendezzük ezt nullára:
`\mathbf{A}\mathbf{v}-lambda \mathbf{v}=\mathbf{0}`
`(\mathbf{A}-lambda\mathbf{I}) \mathbf{v}=\mathbf{0}`
`([[2,-1,-2],[0,0,-1],[0,0,-1]]-[[lambda,0,0],[0,lambda,0],[0,0,lambda]])[[v_x],[v_y],[v_z]]=[[0],[0],[0]]`
`[[2-lambda,-1,-2],[0,-lambda,-1],[0,0,-1-lambda]][[v_x],[v_y],[v_z]]=[[0],[0],[0]]`
Ennek az egyenletnek csak akkor van a triviális `\mathbf{v}=\mathbf{0}` eseten kívüli megoldása, ha a mátrix determinánsa nulla. A determinánst érdemes az utolsó sor szerint kifejteni, mivel abban van a legtöbb nulla:
`|[2-lambda,-1,-2],[0,-lambda,-1],[0,0,-1-lambda]|``=``(-1-lambda)|[2-lambda,-1],[0,-lambda]|``=``(-1-lambda)(2-lambda)(-lambda)=0`
Ez egy harmadfokú egyenlet, de szerencsére már szorzatalakban van, könnyen leolvashatók a megoldások (vagyis a sajátértékek): `lambda_1=0`, `lambda_2=-1` és `lambda_3=2`.
A sajátvektorok az `(\mathbf{A}-lambda\mathbf{I}) \mathbf{v}=\mathbf{0}` egyenlet megoldásával határozhatók meg. `lambda` helyére behelyettesítjük külön-külön az előbb megkapott sajátértékeket, így három sima egyenletrendszert kell megoldani. Fontos tudni, hogy a sajátvektorok nem egyértelműek, egy konstans szorzó erejéig határozatlanok (ha `\mathbf{v}` sajátvektor, akkor `c*\mathbf{v}` is).
Nézzük a `lambda_1=0` sajátértékhez tartozó `\mathbf{v}_1` sajátvektort:
`[[2,-1,-2],[0,0,-1],[0,0,-1]][[v_{1x}],[v_{1y}],[v_{1z}]]=[[0],[0],[0]]`
Az utolsó két egyenlet alapján `v_{1z}=0`, ezután az első egyenlet szerint `2v_{1x}-v_{1y}=0`. Legyen mondjuk `v_{1x}=1`, ekkor `v_{1y}=2`. Tehát a sajátvektor:
`\mathbf{v}_1=[[1],[2],[0]]`
Nézzük a `lambda_2=-1` sajátértékhez tartozó `\mathbf{v}_2` sajátvektort:
`[[3,-1,-2],[0,1,-1],[0,0,0]][[v_{2x}],[v_{2y}],[v_{2z}]]=[[0],[0],[0]]`
A második egyenlet szerint `v_{2y}=v_{2z}`, legyen ez `t`. Ezután az első egyenlet `3v_{2x}-t-2t=0`, amiből `v_{2x}=t`. Azt kaptuk, hogy mindhárom komponens egyenlő, legyen például `1`. Így a sajátvektor:
`\mathbf{v}_2=[[1],[1],[1]]`
Nézzük a `lambda_3=2` sajátértékhez tartozó `\mathbf{v}_3` sajátvektort:
`[[0,-1,-2],[0,-2,-1],[0,0,-3]][[v_{3x}],[v_{3y}],[v_{3z}]]=[[0],[0],[0]]`
Az utolsó egyenlet szerint `v_{3z}=0`, ezután a második egyenletből `v_{3y}=0`, a `v_{3x}` komponens pedig teljesen határozatlan, legyen mondjuk `1`. Tehát az utolsó sajátvektor:
`\mathbf{v}_3=[[1],[0],[0]]`
Kérdés volt még az `\mathbf{A}^20` hatványmátrix. Ehhez érdemes diagonalizálni a mátrixot, más szóval elkészíteni a sajátfelbontását. Ennek feltétele, hogy a sajátvektorok lineárisan függetlenek legyenek, most azok (ha be szeretnéd látni, akkor Gauss-elimináld a sajátvektorokból készített mátrixot, azt fogod kapni, hogy teljes rangú). A sajátfelbontás alakja a következő: `\mathbf{A}=\mathbf{S}\mathbf{Lambda}\mathbf{S}^{-1}`, ahol `\mathbf{S}` a sajátvektorokból alkotott mátrix, `\mathbf{Lambda}` pedig a sajátértékekből alkotott diagonális mátrix. Tehát jelen esetben:
`\mathbf{A}=\mathbf{S}\mathbf{Lambda}\mathbf{S}^{-1}``=``[[1,1,1],[2,1,0],[0,1,0]]*[[0,0,0],[0,-1,0],[0,0,2]]*[[1,1,1],[2,1,0],[0,1,0]]^{-1}``=``[[1,1,1],[2,1,0],[0,1,0]]*[[0,0,0],[0,-1,0],[0,0,2]]*[[0,1/2,-1/2],[0,0,1],[1,-1/2,-1/2]]`
Ez arra jó, hogy a sajátfelbontás segítségével nagyon könnyen ki lehet számolni a hatványmátrixokat, ugyanis `\mathbf{A}^20=\mathbf{S} \mathbf{Lambda}^20 \mathbf{S}^{-1}`, diagonális mátrixot pedig elemenként lehet hatványozni. Tehát:
`\mathbf{A}^20=\mathbf{S}\mathbf{Lambda}^20 \mathbf{S}^{-1}``=``[[1,1,1],[2,1,0],[0,1,0]]*[[0,0,0],[0,(-1)^20,0],[0,0,2^20]]*[[0,1/2,-1/2],[0,0,1],[1,-1/2,-1/2]]``=``[[1048576,-524288,-524287],[0,0,1],[0,0,1]]`
`\mathbf{A}\mathbf{v}-lambda \mathbf{v}=\mathbf{0}`
`(\mathbf{A}-lambda\mathbf{I}) \mathbf{v}=\mathbf{0}`
`([[2,-1,-2],[0,0,-1],[0,0,-1]]-[[lambda,0,0],[0,lambda,0],[0,0,lambda]])[[v_x],[v_y],[v_z]]=[[0],[0],[0]]`
`[[2-lambda,-1,-2],[0,-lambda,-1],[0,0,-1-lambda]][[v_x],[v_y],[v_z]]=[[0],[0],[0]]`
Ennek az egyenletnek csak akkor van a triviális `\mathbf{v}=\mathbf{0}` eseten kívüli megoldása, ha a mátrix determinánsa nulla. A determinánst érdemes az utolsó sor szerint kifejteni, mivel abban van a legtöbb nulla:
`|[2-lambda,-1,-2],[0,-lambda,-1],[0,0,-1-lambda]|``=``(-1-lambda)|[2-lambda,-1],[0,-lambda]|``=``(-1-lambda)(2-lambda)(-lambda)=0`
Ez egy harmadfokú egyenlet, de szerencsére már szorzatalakban van, könnyen leolvashatók a megoldások (vagyis a sajátértékek): `lambda_1=0`, `lambda_2=-1` és `lambda_3=2`.
A sajátvektorok az `(\mathbf{A}-lambda\mathbf{I}) \mathbf{v}=\mathbf{0}` egyenlet megoldásával határozhatók meg. `lambda` helyére behelyettesítjük külön-külön az előbb megkapott sajátértékeket, így három sima egyenletrendszert kell megoldani. Fontos tudni, hogy a sajátvektorok nem egyértelműek, egy konstans szorzó erejéig határozatlanok (ha `\mathbf{v}` sajátvektor, akkor `c*\mathbf{v}` is).
Nézzük a `lambda_1=0` sajátértékhez tartozó `\mathbf{v}_1` sajátvektort:
`[[2,-1,-2],[0,0,-1],[0,0,-1]][[v_{1x}],[v_{1y}],[v_{1z}]]=[[0],[0],[0]]`
Az utolsó két egyenlet alapján `v_{1z}=0`, ezután az első egyenlet szerint `2v_{1x}-v_{1y}=0`. Legyen mondjuk `v_{1x}=1`, ekkor `v_{1y}=2`. Tehát a sajátvektor:
`\mathbf{v}_1=[[1],[2],[0]]`
Nézzük a `lambda_2=-1` sajátértékhez tartozó `\mathbf{v}_2` sajátvektort:
`[[3,-1,-2],[0,1,-1],[0,0,0]][[v_{2x}],[v_{2y}],[v_{2z}]]=[[0],[0],[0]]`
A második egyenlet szerint `v_{2y}=v_{2z}`, legyen ez `t`. Ezután az első egyenlet `3v_{2x}-t-2t=0`, amiből `v_{2x}=t`. Azt kaptuk, hogy mindhárom komponens egyenlő, legyen például `1`. Így a sajátvektor:
`\mathbf{v}_2=[[1],[1],[1]]`
Nézzük a `lambda_3=2` sajátértékhez tartozó `\mathbf{v}_3` sajátvektort:
`[[0,-1,-2],[0,-2,-1],[0,0,-3]][[v_{3x}],[v_{3y}],[v_{3z}]]=[[0],[0],[0]]`
Az utolsó egyenlet szerint `v_{3z}=0`, ezután a második egyenletből `v_{3y}=0`, a `v_{3x}` komponens pedig teljesen határozatlan, legyen mondjuk `1`. Tehát az utolsó sajátvektor:
`\mathbf{v}_3=[[1],[0],[0]]`
Kérdés volt még az `\mathbf{A}^20` hatványmátrix. Ehhez érdemes diagonalizálni a mátrixot, más szóval elkészíteni a sajátfelbontását. Ennek feltétele, hogy a sajátvektorok lineárisan függetlenek legyenek, most azok (ha be szeretnéd látni, akkor Gauss-elimináld a sajátvektorokból készített mátrixot, azt fogod kapni, hogy teljes rangú). A sajátfelbontás alakja a következő: `\mathbf{A}=\mathbf{S}\mathbf{Lambda}\mathbf{S}^{-1}`, ahol `\mathbf{S}` a sajátvektorokból alkotott mátrix, `\mathbf{Lambda}` pedig a sajátértékekből alkotott diagonális mátrix. Tehát jelen esetben:
`\mathbf{A}=\mathbf{S}\mathbf{Lambda}\mathbf{S}^{-1}``=``[[1,1,1],[2,1,0],[0,1,0]]*[[0,0,0],[0,-1,0],[0,0,2]]*[[1,1,1],[2,1,0],[0,1,0]]^{-1}``=``[[1,1,1],[2,1,0],[0,1,0]]*[[0,0,0],[0,-1,0],[0,0,2]]*[[0,1/2,-1/2],[0,0,1],[1,-1/2,-1/2]]`
Ez arra jó, hogy a sajátfelbontás segítségével nagyon könnyen ki lehet számolni a hatványmátrixokat, ugyanis `\mathbf{A}^20=\mathbf{S} \mathbf{Lambda}^20 \mathbf{S}^{-1}`, diagonális mátrixot pedig elemenként lehet hatványozni. Tehát:
`\mathbf{A}^20=\mathbf{S}\mathbf{Lambda}^20 \mathbf{S}^{-1}``=``[[1,1,1],[2,1,0],[0,1,0]]*[[0,0,0],[0,(-1)^20,0],[0,0,2^20]]*[[0,1/2,-1/2],[0,0,1],[1,-1/2,-1/2]]``=``[[1048576,-524288,-524287],[0,0,1],[0,0,1]]`
0
-
R2D2: Nagyon szépen köszönöm! 5 éve 0