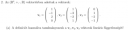Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Lineáris Algebra
 R2D2
kérdése
R2D2
kérdése
476
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Akkor lineárisan független a három vektor, ha a `lambda_1 \mathbf{v}_1+lambda_2 \mathbf{v}_2+lambda_3 \mathbf{v}_3=mathbf{0}` egyenletnek csak a triviális `lambda_1=lambda_2=lambda_3=0` megoldása van. Mátrixos formában felírva az egyenletet:
`[[\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3]][[lambda_1],[lambda_2],[lambda_3]]=\mathbf{0}`
`[[1,1,0],[-1,-3,1],[2,-2,-2],[0,1,-1]][[lambda_1],[lambda_2],[lambda_3]]=[[0],[0],[0],[0]]`
Vagy vizsgálhatjuk az egész transzponáltját is:
`[[lambda_1,lambda_2,lambda_3]][[1,-1,2,0],[1,-3,-2,1],[0,1,-2,-1]]=[[0,0,0,0]]`
Nekem most az utóbbi szimpatikusabb (Gauss-eliminálni fogunk, ilyenkor szeretek minél kevesebb sorral dolgozni). Hozzuk lépcsős alakba a mátrixot. Először vonjuk ki a második sorból az első sort:
`[[1,-1,2,0],[0,-2,-4,1],[0,1,-2,-1]]`
Adjuk hozzá a harmadik sorhoz a második sor felét:
`[[1,-1,2,0],[0,-2,-4,1],[0,0,-4,-1/2]]`
Készen vagyunk: nem tudunk több főegyütthatót kinullázni, nem fogunk csupa nulla sort kapni, a mátrix (és így a vektorrendszer) rangja 3, tehát lineárisan függetlenek a vektorok. Ha teljesen formálisan be akarjuk látni, akkor még tovább mehetünk, és előállíthatjuk a redukált sorlépcsős alakot. Normáljuk az utolsó két sort:
`[[1,-1,2,0],[0,1,2,-1/2],[0,0,1,1/8]]`
Vonjuk ki a harmadik sor kétszeresét az első és a második sorból is:
`[[1,-1,0,-1/4],[0,1,0,-3/4],[0,0,1,1/8]]`
Végül pedig adjuk hozzá a második sort az elsőhöz:
`[[1,0,0,-1],[0,1,0,-3/4],[0,0,1,1/8]]`
Előállt az elején az egységmátrix, ez a redukált sorlépcsős alak. Ha visszaírjuk a teljes egyenletet, akkor ezt azt jelenti, hogy:
`[[lambda_1,lambda_2,lambda_3]][[1,0,0,-1],[0,1,0,-3/4],[0,0,1,1/8]]=[[0],[0],[0],[0]]`
Az első három oszlop azt jelenti, hogy:
`1*lambda_1+0*lambda_2+0*lambda_3=0`
`0*lambda_1+1*lambda_2+0*lambda_3=0`
`0*lambda_1+0*lambda_2+1*lambda_3=0`
Tehát csak a triviális `lambda_1=lambda_2=lambda_3=0` megoldás van, függetlenek a vektorok.
`[[\mathbf{v}_1,\mathbf{v}_2,\mathbf{v}_3]][[lambda_1],[lambda_2],[lambda_3]]=\mathbf{0}`
`[[1,1,0],[-1,-3,1],[2,-2,-2],[0,1,-1]][[lambda_1],[lambda_2],[lambda_3]]=[[0],[0],[0],[0]]`
Vagy vizsgálhatjuk az egész transzponáltját is:
`[[lambda_1,lambda_2,lambda_3]][[1,-1,2,0],[1,-3,-2,1],[0,1,-2,-1]]=[[0,0,0,0]]`
Nekem most az utóbbi szimpatikusabb (Gauss-eliminálni fogunk, ilyenkor szeretek minél kevesebb sorral dolgozni). Hozzuk lépcsős alakba a mátrixot. Először vonjuk ki a második sorból az első sort:
`[[1,-1,2,0],[0,-2,-4,1],[0,1,-2,-1]]`
Adjuk hozzá a harmadik sorhoz a második sor felét:
`[[1,-1,2,0],[0,-2,-4,1],[0,0,-4,-1/2]]`
Készen vagyunk: nem tudunk több főegyütthatót kinullázni, nem fogunk csupa nulla sort kapni, a mátrix (és így a vektorrendszer) rangja 3, tehát lineárisan függetlenek a vektorok. Ha teljesen formálisan be akarjuk látni, akkor még tovább mehetünk, és előállíthatjuk a redukált sorlépcsős alakot. Normáljuk az utolsó két sort:
`[[1,-1,2,0],[0,1,2,-1/2],[0,0,1,1/8]]`
Vonjuk ki a harmadik sor kétszeresét az első és a második sorból is:
`[[1,-1,0,-1/4],[0,1,0,-3/4],[0,0,1,1/8]]`
Végül pedig adjuk hozzá a második sort az elsőhöz:
`[[1,0,0,-1],[0,1,0,-3/4],[0,0,1,1/8]]`
Előállt az elején az egységmátrix, ez a redukált sorlépcsős alak. Ha visszaírjuk a teljes egyenletet, akkor ezt azt jelenti, hogy:
`[[lambda_1,lambda_2,lambda_3]][[1,0,0,-1],[0,1,0,-3/4],[0,0,1,1/8]]=[[0],[0],[0],[0]]`
Az első három oszlop azt jelenti, hogy:
`1*lambda_1+0*lambda_2+0*lambda_3=0`
`0*lambda_1+1*lambda_2+0*lambda_3=0`
`0*lambda_1+0*lambda_2+1*lambda_3=0`
Tehát csak a triviális `lambda_1=lambda_2=lambda_3=0` megoldás van, függetlenek a vektorok.
Módosítva: 5 éve
0
- Még nem érkezett komment!