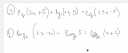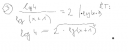Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek logaritmusok
 soósolivér
kérdése
soósolivér
kérdése
342
Valaki lenne olyan kedves, hogy elmagyarázza? 

Jelenleg 1 felhasználó nézi ezt a kérdést.
matek, logaritmus, egyenlet, log
matek, logaritmus, egyenlet, log
0
Középiskola / Matematika
Válaszok
1 rolandstefan
{ Vegyész }
megoldása
rolandstefan
{ Vegyész }
megoldása
Szia!
3-as
`lg(3x+5)+lg(x+5)=lg(43x-5)`, itt fontos kitérni arra, hogy a logaritmus zárójelezett részében (argumentumában), csak nullánál nagyobb szám szerepelhet, kikötéseket kell tenni:
`3x+5>0`, `x>(-5/3)`
`x+5>0`, `x>(-5)`
`43x-5>0`, `x>5/43`
vedd elő a függvénytáblád, keresd meg benne a logaritmusos azonosságokat. Itt ugye a baloldalon két azonos alapú logaritmus összege van, ehhez úgy kell eljárnunk, hogy a két logaritmus utáni zárójelezett részt (argumentumot) összeszorozzuk egy logaritmusban,
amit te látsz: `log_a(b)+log_a(c)=log_a(bc)`, ebben a feladatban az "a"=10 (ugye az lg a tizesalapú logaritmust rövidíti),
"b"=(3x+5), és a "c"=(x+5), ha alkalmazzuk ezt a szabályt:
`lg[(3x+5)*(x+5)]=lg(43x-5)`, ekkor a logaritmus szigorú monotonitására hivatkozva a logaritmusok "eltűnnek", ez lesz:
`(3x+5)*(x+5)=43x-5`, ezzel pedig majd egy másodfokú egyenletet kapsz, amit már könnyű megoldani, a megoldások:
`x_1=6`, `x_2=5/3`, ezek a megoldások megfelelnek a kikötéseinknek, tehát jó megoldások (ha mondjuk -6 lett volna az egyik megoldás, az ugye a kikötéseknek ellentmondott volna, így azt ki kellett volna hagynunk a megoldásokból)
4, feladat:
`log_2(3x-4)-log_2(5)=log_2(x+2)` megint kikötéseket teszünk:
`3x-4>0`, `x>4/3`
`x+2>0`, `x>(-2)`
A bal oldalon azonos alapú logaritmusok különbségét vesszük, ehhez a két logaritmus argumentumának hányadosát kell vennünk, úgy hogy, ami előtt van a negatív előjel az megy a nevezőbe, amit te látsz a fv. táblában:
`log_a(b)-log_a(c)=log_a(b/c)`, ebben a feladatban: "a"=2, "b"=(3x-4), "c"=5, ezt az összefüggést használva az egyenleted:
`log_2[(3x-4)/5]=log_2(x+2)`, itt megint a logaritmus függvény szigorúmonotonitására hivatkozunk, "elhagyjuk" a logaritmust:
`(3x-4)/5=x+2`, ebből a megoldás x=-7 lesz, ezt összevetve a kikötésekkel azt kapjuk, hogy ez nem megoldása az egyenletnek, mivel -2-nél és 4/3-nál is kisebb, tehát ennek az egyenletnek a valós számok halmazán nincs megoldása.
másik 3-as:
`lg(4)/lg(x+1)=2`, itt újból kikötéseket kell tennünk, egyrészt azt, hogy a nevező nem lehet nulla: lg(x+1)≠0, x≠0
x+1>0, x>-1
látom, hogy eljutottál odáig, hogy felviszed a kettest a kitevőbe, onnan folytatom:
`lg(4)=lg(x+1)^2`, itt megint a logaritmus szigorú monotonitására hivatkozunk:
`4=x^2+2x+1`, ebből: `x_1=1`, és `x_2=-3`, ezeket összevetve a kikötésekkel, azt találod, hogy a -3 nem lesz megoldása a valós számok halmazán az egyenletnek, de az 1 igen.
Ezzel vége, remélem nem túl bonyolultan írtam le, bármilyen kérdésed van, nyugodtan írj.
-S.R.
3-as
`lg(3x+5)+lg(x+5)=lg(43x-5)`, itt fontos kitérni arra, hogy a logaritmus zárójelezett részében (argumentumában), csak nullánál nagyobb szám szerepelhet, kikötéseket kell tenni:
`3x+5>0`, `x>(-5/3)`
`x+5>0`, `x>(-5)`
`43x-5>0`, `x>5/43`
vedd elő a függvénytáblád, keresd meg benne a logaritmusos azonosságokat. Itt ugye a baloldalon két azonos alapú logaritmus összege van, ehhez úgy kell eljárnunk, hogy a két logaritmus utáni zárójelezett részt (argumentumot) összeszorozzuk egy logaritmusban,
amit te látsz: `log_a(b)+log_a(c)=log_a(bc)`, ebben a feladatban az "a"=10 (ugye az lg a tizesalapú logaritmust rövidíti),
"b"=(3x+5), és a "c"=(x+5), ha alkalmazzuk ezt a szabályt:
`lg[(3x+5)*(x+5)]=lg(43x-5)`, ekkor a logaritmus szigorú monotonitására hivatkozva a logaritmusok "eltűnnek", ez lesz:
`(3x+5)*(x+5)=43x-5`, ezzel pedig majd egy másodfokú egyenletet kapsz, amit már könnyű megoldani, a megoldások:
`x_1=6`, `x_2=5/3`, ezek a megoldások megfelelnek a kikötéseinknek, tehát jó megoldások (ha mondjuk -6 lett volna az egyik megoldás, az ugye a kikötéseknek ellentmondott volna, így azt ki kellett volna hagynunk a megoldásokból)
4, feladat:
`log_2(3x-4)-log_2(5)=log_2(x+2)` megint kikötéseket teszünk:
`3x-4>0`, `x>4/3`
`x+2>0`, `x>(-2)`
A bal oldalon azonos alapú logaritmusok különbségét vesszük, ehhez a két logaritmus argumentumának hányadosát kell vennünk, úgy hogy, ami előtt van a negatív előjel az megy a nevezőbe, amit te látsz a fv. táblában:
`log_a(b)-log_a(c)=log_a(b/c)`, ebben a feladatban: "a"=2, "b"=(3x-4), "c"=5, ezt az összefüggést használva az egyenleted:
`log_2[(3x-4)/5]=log_2(x+2)`, itt megint a logaritmus függvény szigorúmonotonitására hivatkozunk, "elhagyjuk" a logaritmust:
`(3x-4)/5=x+2`, ebből a megoldás x=-7 lesz, ezt összevetve a kikötésekkel azt kapjuk, hogy ez nem megoldása az egyenletnek, mivel -2-nél és 4/3-nál is kisebb, tehát ennek az egyenletnek a valós számok halmazán nincs megoldása.
másik 3-as:
`lg(4)/lg(x+1)=2`, itt újból kikötéseket kell tennünk, egyrészt azt, hogy a nevező nem lehet nulla: lg(x+1)≠0, x≠0
x+1>0, x>-1
látom, hogy eljutottál odáig, hogy felviszed a kettest a kitevőbe, onnan folytatom:
`lg(4)=lg(x+1)^2`, itt megint a logaritmus szigorú monotonitására hivatkozunk:
`4=x^2+2x+1`, ebből: `x_1=1`, és `x_2=-3`, ezeket összevetve a kikötésekkel, azt találod, hogy a -3 nem lesz megoldása a valós számok halmazán az egyenletnek, de az 1 igen.
Ezzel vége, remélem nem túl bonyolultan írtam le, bármilyen kérdésed van, nyugodtan írj.
-S.R.
0
- Még nem érkezett komment!