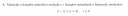Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
ábrázolja a komplex számsíkon azoknak a z komplex számoknak a halmazát, amelyekre
 astaw41
kérdése
astaw41
kérdése
556
ábrázolja a komplex számsíkon azoknak a z komplex számoknak a halmazát, amelyekre
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
Átírod z-t a+bi alakra, ahol a;b valós számok, i pedig a komplex egységgyök, ekkor:
|a+bi-i|≤|a+bi+3|, kicsit rendezzük:
|a+i*(b-1)|≤|a+3+bi|.
Tudjuk, hogy az c+di alakú komplex szám abszolutértéke √ c²+d² , ezt használva:
√ a²+(b-1)² ≤√ (a+3)²+b² , négyzetre emelünk:
a²+(b-1)²≤(a+3)²+b², kibontjuk a zárójeleket:
a²+b²-2b+1≤a²+6a+9+b², kiesnek a négyzetes tagok:
-2b+1≤+6a+9, kivonunk 1-et és osztunk (-2)-vel, fordul a reláció:
b≥-3a-4
Az a;b tengelyű komplex számsík megfelel az x;y tengelyű koordináta-rendszernek, tehát a megoldás is hasonló lesz; ábrázolni kell a -3a-4 lineáris függvényt, és mivel ez kisebb b-nél, vagyis a függvényértéknél, ezért az egyenes feletti részt kell beszínezni, tehát a megoldáshalmaz egy félsík lesz.
|a+bi-i|≤|a+bi+3|, kicsit rendezzük:
|a+i*(b-1)|≤|a+3+bi|.
Tudjuk, hogy az c+di alakú komplex szám abszolutértéke √ c²+d² , ezt használva:
√ a²+(b-1)² ≤√ (a+3)²+b² , négyzetre emelünk:
a²+(b-1)²≤(a+3)²+b², kibontjuk a zárójeleket:
a²+b²-2b+1≤a²+6a+9+b², kiesnek a négyzetes tagok:
-2b+1≤+6a+9, kivonunk 1-et és osztunk (-2)-vel, fordul a reláció:
b≥-3a-4
Az a;b tengelyű komplex számsík megfelel az x;y tengelyű koordináta-rendszernek, tehát a megoldás is hasonló lesz; ábrázolni kell a -3a-4 lineáris függvényt, és mivel ez kisebb b-nél, vagyis a függvényértéknél, ezért az egyenes feletti részt kell beszínezni, tehát a megoldáshalmaz egy félsík lesz.
0
- Még nem érkezett komment!