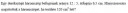Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valaki tudna segíteni?
 Pacal
kérdése
Pacal
kérdése
364
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 Nagy-Gombás Szilvi
{ Tanár }
megoldása
Nagy-Gombás Szilvi
{ Tanár }
megoldása
A derékszögű háromszög befogói: a és b, átfogója c.
Akkor: a : b =12 : 5
c = 6,5 cm
a = 12x
b = 5x
A derékszögű háromszögre alkalmazzuk Pitagorasz-tételét:
a2 + b2 = c2
(12x)2 + (5x)2 = 6,52
144x2 + 25x2 = 42,25
169x2 = 42,25
x2 = 0,25
x = √ 0,25 = 0,5
Akkor megkaptuk a háromszög oldalait:
a = 12 * 0,5 = 6 cm
b = 5 * 0,5 = 2,5 cm
Az eredeti háromszög területe: T = (a * b) / 2 = (6 * 2,5) / 2 = 7,5 cm2
Tehát az eredeti terület 7,5 cm2 , az új háromszög területe 120 cm2.
A területek aránya: 120 / 7,5 = 16, azaz az új háromszög területe az eredeti háromszög 16-szorosa.
Tudjuk azt., hogy hasonló síkidomok területének aránya megegyezik az oldalak arányának négyzetével.
Ez azt jelenti, hogy ha a területek aránya 16, akkor az oldalak aránya √ 16 = 4 lett.
Tehát a háromszög oldalait a 4-szeresére nagyítottuk.
Akkor: a : b =12 : 5
c = 6,5 cm
a = 12x
b = 5x
A derékszögű háromszögre alkalmazzuk Pitagorasz-tételét:
a2 + b2 = c2
(12x)2 + (5x)2 = 6,52
144x2 + 25x2 = 42,25
169x2 = 42,25
x2 = 0,25
x = √ 0,25 = 0,5
Akkor megkaptuk a háromszög oldalait:
a = 12 * 0,5 = 6 cm
b = 5 * 0,5 = 2,5 cm
Az eredeti háromszög területe: T = (a * b) / 2 = (6 * 2,5) / 2 = 7,5 cm2
Tehát az eredeti terület 7,5 cm2 , az új háromszög területe 120 cm2.
A területek aránya: 120 / 7,5 = 16, azaz az új háromszög területe az eredeti háromszög 16-szorosa.
Tudjuk azt., hogy hasonló síkidomok területének aránya megegyezik az oldalak arányának négyzetével.
Ez azt jelenti, hogy ha a területek aránya 16, akkor az oldalak aránya √ 16 = 4 lett.
Tehát a háromszög oldalait a 4-szeresére nagyítottuk.
1
- Még nem érkezett komment!
 markokaa.markokaa
válasza
markokaa.markokaa
válasza
Felírjuk a következő egyenletet a Pitagorasz-tétel alkalmazásával: (12x)^2+(5x)^2=6,5^2 továbbszámolva kijön, hogy 144x^2+25x^2=42,25 tovább 169x^2=42,25 osztunk 169-cel és megkapjuk, hogy x^2=1/4 most pedig gyököt vonunk és megkapjuk, hogy x=1/2 vagyis 0,5 az a=12x=6 cm, b=5x=2,5 cm. A háromszög terület képlete a következő (alap*magasság)/2
Írjuk fel a területképletet: (2,5*6)/2=7,5 tehát az eredeti háromszögünk területe 7,5 cm^2 volt. Ki kell számolnunk, hogy a nagyított háromszög hányszorosa az eredetinek, így 120/7,5=16 A nagyított háromszög tehát az eredeti 16 szorosa. Igaz az eredeti háromszöget 16 szorosára nagyítottuk, de az oldalakat nem. Síkidomoknál az oldalak arányának négyzete megegyezik a terület arányával, ebből következik, hogy gyök 16-tal növeltük az oldalak hosszát, ami 4.
Írjuk fel a területképletet: (2,5*6)/2=7,5 tehát az eredeti háromszögünk területe 7,5 cm^2 volt. Ki kell számolnunk, hogy a nagyított háromszög hányszorosa az eredetinek, így 120/7,5=16 A nagyított háromszög tehát az eredeti 16 szorosa. Igaz az eredeti háromszöget 16 szorosára nagyítottuk, de az oldalakat nem. Síkidomoknál az oldalak arányának négyzete megegyezik a terület arányával, ebből következik, hogy gyök 16-tal növeltük az oldalak hosszát, ami 4.
0
- Még nem érkezett komment!