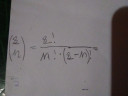Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Házi
 markokaa.markokaa
kérdése
markokaa.markokaa
kérdése
228
Hányféleképpen oszthatunk szét "n" db egyforma könyvet "k" db diáknak?
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 kazah
válasza
kazah
válasza
Elsőre azt gondolnánk, hogy `((k),(n))` a megoldás, de vizsgáljuk meg alaposabban.
Ellenőrizzük le egy egyszerű számítással:
5 egyforma könyvet osztunk szét 5 tanulónak. Ha `((k),(n))` lenne, akkor `((5),(5))` = 1-féle lehetőség van, pedig
tudjuk, hogy nem. Lehet, hogy mindenki kap 1 könyvet; lehet, hogy az összeset egy tanuló kapja és ezek között
bármi. Arról nem beszélve, hogy ha több könyvet sorsolunk ki, mint ahány tanuló van, akkor mi a megoldás.
Az ismétléses kombináció egy kicsit trükkös. Hogy kit mi szerint ismételünk, az kiderül a feladatból, egyik
megközelítésben:
Rakjuk sorba a tanulókat (maradhatunk az 5 könyv 5 tanulónál; A tanulók legyenek A, B, C, D, E). Mindenki tartsa a
bal kezében a kapott könyvet. Sok lehetőség van, itt egy pár:
K A K B K C K D K E `rightarrow` Mindenki kapott 1 könyvet
K A K K B C D K K E `rightarrow` A egyet, B kettőt, E kettőt
A K B K K C K K D E `rightarrow` B egyet, C és D kettőt
K K K K K A B C D E `rightarrow` Mindet A kapta
A K K K B C D K K E `rightarrow` B hármat, E kettőt
Azért írtam fel többet, hogy lássuk, a jobb oldalra mindig E kerül, vele nem kell számolnunk, a többi helyre
kerülhet bármi. Így összesen csak 9 elemünk van, amit kombinálhatunk és van benne 5 azonos, így egy 9 elem 5-ödosztályú ismétlés nélküli kombinációját kapjuk.
`C_9^5` = `((9),(5))` = `(9!)/(4!*5!)` = `(6*7*8*9)/(2*3*4)` = 126 féleképpen kaphatják a könyvet.
A konkrét példánál maradva:
Van n darab egyforma könyvünk és k darab diákunk, ez összesen n+k elem, szépen sorba rakjuk őket, ahogy fentebb, az
utolsó diák mindig jobb oldalra kerül, így egy (n+k-1) elem n-edosztályú ismétlés nélküli kombinációját kell
megoldanunk:
`C_n^(k,i)` = `C_n^(n+k-1)` = `((n+k-1),(n))` = `((n+k-1)!)/(n!*(k-1)!)`
Az `((n),(k))` akkor lenne igaz, ha minden tanuló csak 1 könyvet kapna. (Az 5 tanuló 5 könyvből ez látszik is, 1 ilyen eset van)
Ellenőrizzük le egy egyszerű számítással:
5 egyforma könyvet osztunk szét 5 tanulónak. Ha `((k),(n))` lenne, akkor `((5),(5))` = 1-féle lehetőség van, pedig
tudjuk, hogy nem. Lehet, hogy mindenki kap 1 könyvet; lehet, hogy az összeset egy tanuló kapja és ezek között
bármi. Arról nem beszélve, hogy ha több könyvet sorsolunk ki, mint ahány tanuló van, akkor mi a megoldás.
Az ismétléses kombináció egy kicsit trükkös. Hogy kit mi szerint ismételünk, az kiderül a feladatból, egyik
megközelítésben:
Rakjuk sorba a tanulókat (maradhatunk az 5 könyv 5 tanulónál; A tanulók legyenek A, B, C, D, E). Mindenki tartsa a
bal kezében a kapott könyvet. Sok lehetőség van, itt egy pár:
K A K B K C K D K E `rightarrow` Mindenki kapott 1 könyvet
K A K K B C D K K E `rightarrow` A egyet, B kettőt, E kettőt
A K B K K C K K D E `rightarrow` B egyet, C és D kettőt
K K K K K A B C D E `rightarrow` Mindet A kapta
A K K K B C D K K E `rightarrow` B hármat, E kettőt
Azért írtam fel többet, hogy lássuk, a jobb oldalra mindig E kerül, vele nem kell számolnunk, a többi helyre
kerülhet bármi. Így összesen csak 9 elemünk van, amit kombinálhatunk és van benne 5 azonos, így egy 9 elem 5-ödosztályú ismétlés nélküli kombinációját kapjuk.
`C_9^5` = `((9),(5))` = `(9!)/(4!*5!)` = `(6*7*8*9)/(2*3*4)` = 126 féleképpen kaphatják a könyvet.
A konkrét példánál maradva:
Van n darab egyforma könyvünk és k darab diákunk, ez összesen n+k elem, szépen sorba rakjuk őket, ahogy fentebb, az
utolsó diák mindig jobb oldalra kerül, így egy (n+k-1) elem n-edosztályú ismétlés nélküli kombinációját kell
megoldanunk:
`C_n^(k,i)` = `C_n^(n+k-1)` = `((n+k-1),(n))` = `((n+k-1)!)/(n!*(k-1)!)`
Az `((n),(k))` akkor lenne igaz, ha minden tanuló csak 1 könyvet kapna. (Az 5 tanuló 5 könyvből ez látszik is, 1 ilyen eset van)
Módosítva: 5 éve
0
- Még nem érkezett komment!