Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
12.osztály
 Nagybela
kérdése
Nagybela
kérdése
693
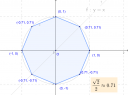
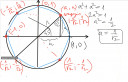
A derékszögű koordináta-rendszerben az origó középpontú egységsugarú körbe írt szabályos nyolcszög egyik csúcsának koordinátái (1; 0). Határozzuk meg a többi csúcs koordinátáit!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
3 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
Egységnyi sugarú, origó középpontú kör.
K (0 ; 0)
r = 1
A kör egyenlete: x2 + y2 = 1
Ezen a körön helyezkednek el a nyolcszög csúcspontjai.
Az egyik csúcspont: A ( 1 ; 0)
Ha a csúcspontokba behúzzuk a kör sugarait, akkor a nyolcszöget 8 db olyan egyenlőszárú háromszögre bontjuk, melyeknek a szárszöge: 360⁰/ 8 = 45⁰-os.
Ez azt jelenti, hogy a körnek az A csúcsból induló átmérőjének a másik végpontja is csúcspont lesz, tehát megvan még egxy csúcspontunk: E ( -1 ; 0)
Tehát 2 szemközti csúcspont az x tengelyre esik. Mivel a szárszögek 45⁰-osak, ezért az y tengelyen is lesz 2 csúcspontja a sokszögnek. C ( 0 , 1) és G ( 0 ; -1).
Mivel a szögek 45⁰-osak a hiányzó 4 csúcspont közül 2 az y = x egyenesen helyezkedik el. Mivel a csúcspontok a körön is rajta vannak, ezért teljesül, hogy
x2 + x2 = 1
2x2 = 1
x2 = 1/2
x = ± √ 1/2 = ± 1/√ 2 = ±√ 2 /2
Akkor: y = ±√ 2 /2
Tehát: B ( √ 2 /2 ; √ 2 /2) és F ( -√ 2 /2 ; -√ 2 /2)
Ugyanígy a hiányzó 2 csúcspont pedig az y = -x egyenesen van rajta.
x2 + (-x)2 = 1
x2 + x2 = 1
2x2 = 1
x2 = 1/2
x = ± √ 1/2 = ± 1/√ 2 = ±√ 2 /2
Így megkaptuk a még hiányzó pontokat:
D ( -√ 2 /2 ; √ 2 /2) és H (√ 2 /2 ; -√ 2 /2)
K (0 ; 0)
r = 1
A kör egyenlete: x2 + y2 = 1
Ezen a körön helyezkednek el a nyolcszög csúcspontjai.
Az egyik csúcspont: A ( 1 ; 0)
Ha a csúcspontokba behúzzuk a kör sugarait, akkor a nyolcszöget 8 db olyan egyenlőszárú háromszögre bontjuk, melyeknek a szárszöge: 360⁰/ 8 = 45⁰-os.
Ez azt jelenti, hogy a körnek az A csúcsból induló átmérőjének a másik végpontja is csúcspont lesz, tehát megvan még egxy csúcspontunk: E ( -1 ; 0)
Tehát 2 szemközti csúcspont az x tengelyre esik. Mivel a szárszögek 45⁰-osak, ezért az y tengelyen is lesz 2 csúcspontja a sokszögnek. C ( 0 , 1) és G ( 0 ; -1).
Mivel a szögek 45⁰-osak a hiányzó 4 csúcspont közül 2 az y = x egyenesen helyezkedik el. Mivel a csúcspontok a körön is rajta vannak, ezért teljesül, hogy
x2 + x2 = 1
2x2 = 1
x2 = 1/2
x = ± √ 1/2 = ± 1/√ 2 = ±√ 2 /2
Akkor: y = ±√ 2 /2
Tehát: B ( √ 2 /2 ; √ 2 /2) és F ( -√ 2 /2 ; -√ 2 /2)
Ugyanígy a hiányzó 2 csúcspont pedig az y = -x egyenesen van rajta.
x2 + (-x)2 = 1
x2 + x2 = 1
2x2 = 1
x2 = 1/2
x = ± √ 1/2 = ± 1/√ 2 = ±√ 2 /2
Így megkaptuk a még hiányzó pontokat:
D ( -√ 2 /2 ; √ 2 /2) és H (√ 2 /2 ; -√ 2 /2)
0
-
Nagybela: Köszönöm, ez nagyon jó magyarázat. Így már érthetőbb! 5 éve 0