Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek házi
 kalinalena3
kérdése
kalinalena3
kérdése
289
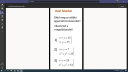
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
2 kazah
megoldása
kazah
megoldása
1, Kifejezzük az első egyenletből az egyik paramétert, majd behelyettesítjük a másodikba:
I. y = 12-x
II. x(12-x) = 35
12x-`x^2` = 35
`x^2`-12x+35 = 0
szorzattá alakítjuk vagy megoldóképlet.
(x-5)(x-7) = 0
`x_1` = 5; y_1 = 7
`x_2` = 7; `y_2` = 5
Az ellenőrzést már meg tudod oldani.
2,
mint az elsőnél
I. y = 7-x
II. `x^2`+`(7-x)^2` = 25
`2x^2-14x+49 = 25`
`2x^2-14x-24` = 0
`x^2-7x+12` = 0
(x-3)(x-4) = 0
`x_1` = 3; `y_1` = 4
`x_2` = 4; `y_2` = 3
3,
Itt lehet kicsit trükközni, nevezetes azonossággá alakítjuk.
I. (*2) 2xy = 48
Ezt hozzáadjuk a második egyenlethez:
`x^2+2xy+y^2` = (48+52=) 100
`(x+y)^2` = 100
innen két út van,
a, Ha x+y = 10
I. xy = 24
x(10-x) = 24
`x^2-10x+24` = 0
(x-6)(x-4) = 0
`x_1` = 6; `y_1` = 4
`x_2` = 4; `y_2` = 6
b, Ha x+y = -10
I. xy = 24
x(-10-x) = 24
`x^2+10x+24` = 0
`(x+6)(x+4)` = 0
`x_3` = -6; `y_3` = -4
`x_4` = -4; `y_4` = -6
1
- Még nem érkezett komment!
 lele21
{ Tanár }
válasza
lele21
{ Tanár }
válasza
Photomath alkalmazás tud segíteni máskor (is). Levezeti a feladatot érthetően szöveggel!
-1
- Még nem érkezett komment!