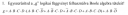Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Boole Algebra
 R2D2
kérdése
R2D2
kérdése
254
Valaki esetlegleg le ellenőrizné és ahol nem jó kijavítana ?
Ha kérhetem legyen lépésről lépésre írva , hogy tudja relatíve egyszerűen észre venni a hibám.
Válaszokat előre is köszönöm!
Ha kérhetem legyen lépésről lépésre írva , hogy tudja relatíve egyszerűen észre venni a hibám.
Válaszokat előre is köszönöm!
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Felsőoktatás / Matematika
Válaszok
1 AlBundy
{ Polihisztor }
megoldása
AlBundy
{ Polihisztor }
megoldása
Helyesen felismerted, hogy az `A A B B C C D bar D` tagban `D` és `bar D` sosem lehet egyszerre igaz, tehát az ÉS kapcsolatuk hamis. Viszont így az egész tag kiesik, hiszen `A A B B C C * 0 =0`. Ugyanígy kiesik a második és a harmadik tag is, és csak `g=A A B B C C D D + A B bar D` marad, azaz egyszerűsítve `g=ABCD+A B bar D`. Kiemelve a közös tényezőket: `g=A B (C D+bar D)`. A zárójeles részből `D` elhagyható, és a végeredmény `g=AB(C+bar D)`, avagy kibontva (diszjunktív alakban) `g=ABC+AB bar D`.
A végén felhasznált `CD+bar D = C+ bar D` azonosság többféleképpen is belátható. Egyrészt végig lehet, gondolni, hogy ha `D=1`, akkor a kifejezés értéke `C*1+0=C`, ha pedig `D=0`, akkor a kifejezés értéke `C*0+1=1`, tehát összességében éppen `C+bar D`. Formálisan belátható úgy, hogy a `bar D` taghoz ÉS kapcsolattal hozzáfűzzük az `1+C` értéket. Ez mindig igaz, tehát nem rontottunk el semmit:
`CD+bar D=CD + bar D (1+C)=CD+bar D + C bar D=C(D+ bar D)+bar D=C*1+bar D=C + bar D`
A harmadik lehetőség, hogy kétszer egymás után invertáljuk a de Morgan-formulákkal:
`bar{CD + bar D}=bar{CD}*D=(bar C + bar D)D=barC D + bar D D=bar C D`
`bar{bar C D }=C + bar D`
Egyébként sajnos a többi átalakításod is hibás, például a `BD +A+A B bar D` sorból nem az következik, hogy `BD+(A+A)B bar D`, hanem a kiemelés helyesen `BD+A(1+B bar D)=BD+A`.
A végén felhasznált `CD+bar D = C+ bar D` azonosság többféleképpen is belátható. Egyrészt végig lehet, gondolni, hogy ha `D=1`, akkor a kifejezés értéke `C*1+0=C`, ha pedig `D=0`, akkor a kifejezés értéke `C*0+1=1`, tehát összességében éppen `C+bar D`. Formálisan belátható úgy, hogy a `bar D` taghoz ÉS kapcsolattal hozzáfűzzük az `1+C` értéket. Ez mindig igaz, tehát nem rontottunk el semmit:
`CD+bar D=CD + bar D (1+C)=CD+bar D + C bar D=C(D+ bar D)+bar D=C*1+bar D=C + bar D`
A harmadik lehetőség, hogy kétszer egymás után invertáljuk a de Morgan-formulákkal:
`bar{CD + bar D}=bar{CD}*D=(bar C + bar D)D=barC D + bar D D=bar C D`
`bar{bar C D }=C + bar D`
Egyébként sajnos a többi átalakításod is hibás, például a `BD +A+A B bar D` sorból nem az következik, hogy `BD+(A+A)B bar D`, hanem a kiemelés helyesen `BD+A(1+B bar D)=BD+A`.
0
- Még nem érkezett komment!