Tehát az ABCD húrnégyszögről beszélünk. Ha igaz az állítás, akkor a BOD törött vonalról is
elmondhatjuk ugyanezt, mert A és C pontpár nincs kitüntetett helyzetben a B és a D pontokhoz
képest.

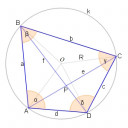
Felhasználunk egy segédtételt, ha `AC bot BD`, akkor
`a^2+c^2=b^2+d^2=4R^2`, ahol R a húrnégyszög köré
írt kör sugara. (lásd a csatolt képet)
Továbbá tudjuk, hogy `T_(ABCD)=frac{e*f}{2}=frac{b*d+a*c}{2}`
`DOC triangle` egyenlőszárú háromszög,
innen Pitagorasz-tétellel felhasználjuk, hogy `c^2+4*m_c^2=4*R^2`,
ahonnan `2*m_c=a`. `AOD triangle` egyenlőszárú háromszög,
innen Pitagorasz-tétellel felhasználjuk, hogy `a^2+4*m_a^2=4*R^2`,
ahonnan `2*m_a=c`.

`2*c*m_c=2*a*m_a=a*c`
Hasonlóan gondolkozva
`2*b*m_b=2*d*m_d=b*d`
`T_(AOCD)=T_(AOD)+T_(DOC)=frac{b*d+a*c}{4]=frac{T_(ABCD)}{2}`
Hasonló gondolkodással `T_(BODA)=frac{T_(ABCD)}{2}`is igaz állítás lesz.
q. e. d.

Kérdés még, hogy a fent idézett segédtételt a bizonyítással együtt tanultátok-e
az iskolában? Ha nem ismered az állítást, akkor reagálj erre, hogy a hiányosság
pótlására is legyen idő.

Hm...

Miközben kerestem a segédtételre a bizonyítást, találtam
az állításodra egy másik (rövidebb) levezetést is.

Másik bizonyítás: Legyen `AOB angle =mu` és `COD angle=nu`.
Ekkor `ADP angle=mu/2` és `PAD angle=nu/2`, mert ugyanahhoz
körívhez tartozó középponti és kerületi szögekhez tartoznak.
Ekkor`mu+nu=180°`,`T_(AOB)=R^2*sin(mu)/2` és `T_(COD)=R^2*sin(nu)/2`.
Mivel `sin(mu)=sin(180°-mu)=sin(nu)`adódik, hogy
`T_(AOB)=T_(COD)`. Hasonló gondolatmenettel `T_(AOD)=T_(BOC)`.
Innen már levezethető a bizonyítandó állításod.
q.e.d.

A segédtétel bizonyítása: Felhasználva az előbbi jelöléseket
Legyen `AOB angle =mu` és `COD angle=nu` és hosszabítsuk meg `AO`
félegyenest, amely körívet egy másik `X` pontban metszi.
Vizsgálva az `AXB` derékszögű háromszöget kapjuk, hogy
`AB=2*R*sin(mu/2)` és `BX=2*R*cos(mu/2)`. Mivel a `BX`
húr ugyanahhoz a `nu` középponti szöghöz tartozik, mint a `CD` húr,
ezért `BX=CD`. Így `AB^2+CD^2=4*R^2*(sin^2(mu/2)+cos^2(mu/2))=`
`=a^2+c^2=4*R^2`. Hasonló okoskodással nyerhető
a `b^2+d^2=4*R^2` összefüggés is. q.e.d.