Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Matek 10
 koloszvar345
kérdése
koloszvar345
kérdése
518
Csatoltam képet.
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
7 Nagy-Gombás Szilvi
{ Tanár }
megoldása
Nagy-Gombás Szilvi
{ Tanár }
megoldása
1. feladat:
A függvénynek ott van zérushelye, ahol metszi az x-tengelyt, vagyis, ahol a függvény hozzárendelési utasítása egyenlő 0-val.
|x|-1=0
|x|=1 -> x1=1 x2=-1
Mindkét eredmény benne van az értelmezési tartományban, tehát -1 és 1 is zérushelyek.
A függvénynek ott van zérushelye, ahol metszi az x-tengelyt, vagyis, ahol a függvény hozzárendelési utasítása egyenlő 0-val.
|x|-1=0
|x|=1 -> x1=1 x2=-1
Mindkét eredmény benne van az értelmezési tartományban, tehát -1 és 1 is zérushelyek.
2
- Még nem érkezett komment!
 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
2. feladat:
A gondolt szám: x
A gondolt szám fele: x/2
A gondolt szám feléből kivonunk 5-öt: x/2-5
A különbséget megszorozzuk 4-gyel: (x/2-5)*4
A kapott számhoz hozzáadunk 8-at: (x/2-5)*4+8
Az egyenlet:
(x/2-5)*4+8=x/2
Rendezzük az egyenletet!
2x-20+8=x/2
2x-12=x/2 /*2
4x-24=x /-4x
-24=-3x /:(-3)
8=x
A gondolt szám a 8.
Ellenőrzés:
A gondolt szám fele: x/2 =4
A gondolt szám feléből kivonunk 5-öt: x/2-5 =-1
A különbséget megszorozzuk 4-gyel: (x/2-5)*4 = -4
A kapott számhoz hozzáadunk 8-at: (x/2-5)*4+8 = 4 4 pedig a gondolt szám fele, tehát a megoldás jó.
A gondolt szám: x
A gondolt szám fele: x/2
A gondolt szám feléből kivonunk 5-öt: x/2-5
A különbséget megszorozzuk 4-gyel: (x/2-5)*4
A kapott számhoz hozzáadunk 8-at: (x/2-5)*4+8
Az egyenlet:
(x/2-5)*4+8=x/2
Rendezzük az egyenletet!
2x-20+8=x/2
2x-12=x/2 /*2
4x-24=x /-4x
-24=-3x /:(-3)
8=x
A gondolt szám a 8.
Ellenőrzés:
A gondolt szám fele: x/2 =4
A gondolt szám feléből kivonunk 5-öt: x/2-5 =-1
A különbséget megszorozzuk 4-gyel: (x/2-5)*4 = -4
A kapott számhoz hozzáadunk 8-at: (x/2-5)*4+8 = 4 4 pedig a gondolt szám fele, tehát a megoldás jó.
2
- Még nem érkezett komment!
 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
3. feladat:
Az adott függvény: f(x)= 0,0001x2-0,0063x+15,2
2000-ben a középhőmérséklet:
1900-tól 99 év telt el 2000-ig, tehát x=99. Ezt behelyettesítve f(x)-be kapjuk, hogy:
f(99)= 0,0001*992 - 0,0063*99 + 15,2 = 15,5564 ⁰C
Tehát 2000-ben 15,5554 ⁰C volt a középhőmérséklet.
2020-ban a középhőmérséklet:
1900-tól 119 év telt el 2020-ig, tehát x=119. Ezt behelyettesítve f(x)-be kapjuk, hogy:
f(119)= 0,00001*1192 - 0,0063*119 + 15,2 = 15,8664 ⁰C
Tehát 2020-ban 15,8664 ⁰C volt a középhőmérséklet.
A 2020-as és 2000-es középhőmérséklet különbsége: 15,8664 ⁰C - 15,5564 ⁰C = 0,31 ⁰C
Vagyis 0,31 ⁰C-kal volt magasabb a középhőmérséklet 2020-ban, mint 2000-ben.
Az adott függvény: f(x)= 0,0001x2-0,0063x+15,2
2000-ben a középhőmérséklet:
1900-tól 99 év telt el 2000-ig, tehát x=99. Ezt behelyettesítve f(x)-be kapjuk, hogy:
f(99)= 0,0001*992 - 0,0063*99 + 15,2 = 15,5564 ⁰C
Tehát 2000-ben 15,5554 ⁰C volt a középhőmérséklet.
2020-ban a középhőmérséklet:
1900-tól 119 év telt el 2020-ig, tehát x=119. Ezt behelyettesítve f(x)-be kapjuk, hogy:
f(119)= 0,00001*1192 - 0,0063*119 + 15,2 = 15,8664 ⁰C
Tehát 2020-ban 15,8664 ⁰C volt a középhőmérséklet.
A 2020-as és 2000-es középhőmérséklet különbsége: 15,8664 ⁰C - 15,5564 ⁰C = 0,31 ⁰C
Vagyis 0,31 ⁰C-kal volt magasabb a középhőmérséklet 2020-ban, mint 2000-ben.
2
- Még nem érkezett komment!
 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
4. a) feladat:
Függvényérték kiszámolása úgy történik, hogy az adott x-et behelyettesítjük a függvény hozzárendelési utasításába.
x = 3 benne van az értelmezési tartományban, tehát létezik hozzá tartozó függvényérték.
Kiszámolása:
f(3) = (3 - 1)2 - 5 = 22 -5 = 4 - 5 = -1
Tehát a függvény a 3-hoz a -1-et rendeli.
Függvényérték kiszámolása úgy történik, hogy az adott x-et behelyettesítjük a függvény hozzárendelési utasításába.
x = 3 benne van az értelmezési tartományban, tehát létezik hozzá tartozó függvényérték.
Kiszámolása:
f(3) = (3 - 1)2 - 5 = 22 -5 = 4 - 5 = -1
Tehát a függvény a 3-hoz a -1-et rendeli.
2
- Még nem érkezett komment!
 Nagy-Gombás Szilvi
{ Tanár }
válasza
Nagy-Gombás Szilvi
{ Tanár }
válasza
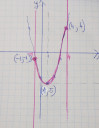
4. b) feladat:
Ábrázolás: csatoltam képet.
Jellemzés:
Monotonítás:
A grafikon alapján a függvény a [-1 ; 1[ intervallumon szigorúan monoton csökkenő, az ]1; 4] intervallumon szigorúan monoton növekvő. (x-tengelyen nézzük)
Szésőérték:
A függvénynek minimuma van x = 1 helyen, ahol a minimumérték f(1) = -5.
Tehát az (1 ; -5) pontban van a függvénynek minimuma.
Zérushely: Ott van, ahol a függvény hozzárendelési utasítása egyenlő 0-val, azaz
(x - 1)2 - 5 = 0
( x - 1)2= 5
x - 1 = ± √ 5
x = 1 ±√ 5
Az 1 - √ 5 nincs benne az értelmezési tartományban, tehát a függvénynek 1 zérushelye van, az x = 1 + √ 5 .
Értékkészlet: A függvény milyen értékeket vesz fel az y-tengelyen.
ÉK.: (vagy Rf) y∈[-5 ; 4]
Ábrázolás: csatoltam képet.
Jellemzés:
Monotonítás:
A grafikon alapján a függvény a [-1 ; 1[ intervallumon szigorúan monoton csökkenő, az ]1; 4] intervallumon szigorúan monoton növekvő. (x-tengelyen nézzük)
Szésőérték:
A függvénynek minimuma van x = 1 helyen, ahol a minimumérték f(1) = -5.
Tehát az (1 ; -5) pontban van a függvénynek minimuma.
Zérushely: Ott van, ahol a függvény hozzárendelési utasítása egyenlő 0-val, azaz
(x - 1)2 - 5 = 0
( x - 1)2= 5
x - 1 = ± √ 5
x = 1 ±√ 5
Az 1 - √ 5 nincs benne az értelmezési tartományban, tehát a függvénynek 1 zérushelye van, az x = 1 + √ 5 .
Értékkészlet: A függvény milyen értékeket vesz fel az y-tengelyen.
ÉK.: (vagy Rf) y∈[-5 ; 4]
Módosítva: 5 éve
2
- Még nem érkezett komment!