Szia!

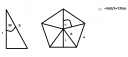
A feladat megoldását a gúla alapjának meghatározásával kezdjük. Csatoltam egy képet segítségképpen.
A te feladatodban r=1m, és M=2m. Láthatod hogy az ötszöget 5db egybevágó egyenlőszárú háromszögre bonthatjuk melyeknek magassága az r. A baloldali derékszögben a függöleges oldal: r=1m, a vízszintes oldal: a/2, a szög: 36⁰. Mivel két befogónk van tangenst használunk: tgα=r/(a/2), amiből a/2=r/tgα=1/tg36⁰=1/0,7265=1,38m. Amiből a=2,76m
A háromszög területe: Tháromszög=a*ma/2=a*r/2=2,76*0,5=1,38m2
Az ötszög területe: Tötszög=5*Tháromszög=5*1,38=6,9m2
A gúla térfogata: V=Tötszög*M/3=6,9*2/3=4,6m3
A güla palástjának területéhez még szükség van az oldalak területére (5db háromszög). Ezeknek az alapja: a, magassága: mo. Azonban mo-t még nem ismerjük.
Ha a gúla magasságát berajzolod a gúlába és a középpontot összekötöd az oldal felezőpontjával, majd a két végpontot egymással egy derékszögű háromszöget kapsz. Ennek oldalai: M=2m, r=1m, mo=?
Pitagorasz tételét használva:
a2+b2=c2
M2+r2=mo2
22+12=mo2
4+1=mo2
5=mo2, amiből mo=2,236m.
Az oldal területe: Toldal=a*mo/2=2,76*2,236/2=3,08m2
A gúla palástjának területe: 5*Toldal=5*3,08=15,4m2