Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Valószínűség SOS
 szg.k9kristof
{ Fortélyos } kérdése
szg.k9kristof
{ Fortélyos } kérdése
1095
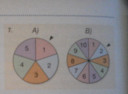
Az ábrán látható két pörgettyűt megforgatjuk, és a kapott számokat összeszorozzuk. Mennyi a valószínűsége, hogy a szorzat
a., kisebb 10-nél
b., páratlan
c., páros
d., 3-mal osztható?
a., kisebb 10-nél
b., páratlan
c., páros
d., 3-mal osztható?
Jelenleg 1 felhasználó nézi ezt a kérdést.
TK.214/7
TK.214/7
0
Általános iskola / Matematika
Válaszok
1 Rantnad
{
Rantnad
{  }
megoldása
}
megoldása
Az első pörgettyűről 1/5, a másodikról 1/10 valószínűséggel pörög ki egy szám.
a) Írjuk fel esetenként oly módon, hogy az első pörgettyűről mi pörög ki:
-ha az 1-es pörög ki, akkor a másikról 1-től 9-ig bármi kipöröghet, ennek valószínűsége (1/5)*(9/10)=9/50.
-ha a 2-es pörög ki, akkor a másikon 1-től 4-ig jöhetnek a számok, ennek valószínűsége (1/5)*(4/10)=4/50 (nem érdemes egyszerűsíteni, mivel úgyis össze kell ezeket adni, és mindegyiknek 50 lesz a nevezője).
-ha 3-as pörög ki, akkor 1-től 3-ig jöhet a másikról, így (1/5)*(3/10)=3/50 a valószínűsége.
-ha 4-es jön, akkor 1 és 2 jöhet a másikról ennek (1/5)*(2/10)=2/50 az esélye
-ha 5-ös jön ki, akkor csak 1 jöhet párnak, így ennek (1/5)*(1/10)=1/50 az esélye.
Ezek összege adja a valószínűséget: (9/50)+(4/50)+(3/50)+(2/50)+(1/50)=19/50=0,38=38%.
b) A szorzat csak úgy lehet páratlan, hogyha mindkét tényezője páratlan; az első pörgettyűről 3/5 eséllyel jön ki páratlan szám, a másodikról 5/10=1/2 valószínűséggel, így annak a valószínűsége, hogy páratlan lesz a szorzat: (3/5)*(1/2)=3/10=0,3=30%.
c) Ha b)-nél 30% volt, akkor ennek 70% lesz az esélye, lévén egymást kizáró események (mivel egy egész eredményű szorzat vagy páros, vagy páratlan).
d) Ezt érdemesebb úgy számolni, hogy hány esetben NEM lesz 3-mal osztható; egy szorzat akkor osztható 3-mal, hogyha valamelyik tényezője osztható 3-mal, így akkor nem osztható, hogyha egyik tényezője sem osztható 3-mal. Az első pörgettyűn 4 ilyen szám van, tehát 4/5 valószínűséggel forog ki 3-mal nem osztható szám, a másodikon 7 ilyen van, így 7/10 valószínűsséggel pörög ki, tehát annak a valószínűsége, hogy 3-mal NEM osztható lesz a szorzat: (4/5)*(7/10)=28/50=14/25=0,56=56%, így annak a valószínűsége, hogy 3-mal osztható szorzatot kapunk: 44%.
Ha valami nem érthető, kérdezz!
a) Írjuk fel esetenként oly módon, hogy az első pörgettyűről mi pörög ki:
-ha az 1-es pörög ki, akkor a másikról 1-től 9-ig bármi kipöröghet, ennek valószínűsége (1/5)*(9/10)=9/50.
-ha a 2-es pörög ki, akkor a másikon 1-től 4-ig jöhetnek a számok, ennek valószínűsége (1/5)*(4/10)=4/50 (nem érdemes egyszerűsíteni, mivel úgyis össze kell ezeket adni, és mindegyiknek 50 lesz a nevezője).
-ha 3-as pörög ki, akkor 1-től 3-ig jöhet a másikról, így (1/5)*(3/10)=3/50 a valószínűsége.
-ha 4-es jön, akkor 1 és 2 jöhet a másikról ennek (1/5)*(2/10)=2/50 az esélye
-ha 5-ös jön ki, akkor csak 1 jöhet párnak, így ennek (1/5)*(1/10)=1/50 az esélye.
Ezek összege adja a valószínűséget: (9/50)+(4/50)+(3/50)+(2/50)+(1/50)=19/50=0,38=38%.
b) A szorzat csak úgy lehet páratlan, hogyha mindkét tényezője páratlan; az első pörgettyűről 3/5 eséllyel jön ki páratlan szám, a másodikról 5/10=1/2 valószínűséggel, így annak a valószínűsége, hogy páratlan lesz a szorzat: (3/5)*(1/2)=3/10=0,3=30%.
c) Ha b)-nél 30% volt, akkor ennek 70% lesz az esélye, lévén egymást kizáró események (mivel egy egész eredményű szorzat vagy páros, vagy páratlan).
d) Ezt érdemesebb úgy számolni, hogy hány esetben NEM lesz 3-mal osztható; egy szorzat akkor osztható 3-mal, hogyha valamelyik tényezője osztható 3-mal, így akkor nem osztható, hogyha egyik tényezője sem osztható 3-mal. Az első pörgettyűn 4 ilyen szám van, tehát 4/5 valószínűséggel forog ki 3-mal nem osztható szám, a másodikon 7 ilyen van, így 7/10 valószínűsséggel pörög ki, tehát annak a valószínűsége, hogy 3-mal NEM osztható lesz a szorzat: (4/5)*(7/10)=28/50=14/25=0,56=56%, így annak a valószínűsége, hogy 3-mal osztható szorzatot kapunk: 44%.
Ha valami nem érthető, kérdezz!

1
- Még nem érkezett komment!