πSzia!

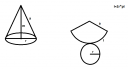
Csatoltam egy képet a magyarázathoz.
1. A kúp palástja egy olyan körcikk ami egy háromszöghőz hasonlít. Ennek az alapja a kör kerülete (2rπ), magassága a kúp alkotója (a). Azonban az a-t nem ismerjük ezért előbb azt kell kiszámolni. A bal oldali ábrán láthatod hogy a kúp magasságának berajzolásával egy derékszögű háromszög keletkezik, ennek oldalai: m=175cm, r=65cm, és az a. Az a lesz a háromszög átfogója,ezért a Pitagorasz tétel így néz ki:
a2+b2=c2
m2+r2=a2
1752+652=a2
30625+4225=a2
34850=a2, amiből a=186,68cm, vagyis a körcikk sugara: 1,86m
2. A körcikkhez tartozó körív ugyanakkora mint az alapkör kerülete: i=2rπ, i azonban felírható az a segítségével is i=2aπ*α/360⁰, ezeket egyenlővé téve: 2rπ=2aπα/360⁰ /:2π
r=a*α/360⁰
65=186*α/360⁰ /:186
0,35=α/360⁰ /*360⁰
126⁰=α, vagyis a középponti szög 126⁰.
3. A palást elkészítéséhez szükséges anyag nagyságát a palást területe jelenti, ami a P=a2π*α/360⁰ képlettel számítható. Behelyettesítve:
P=1862*3,14*126⁰/360⁰=38021,004cm2=3,8m2