Szia!

47a, Egy egyenlőszárú háromszög
A magasság két egybevágó derékszögű háromszögre bontja az eredeti háromszöget. Ennek az oldalai: 1,8cm, 2,4cm és xcm.
Mivel az átfogó a keresett x, ezért Pitagorasz-tétellel (a2+b2=c2):
2,42+1,82=x2
5,76+3,24=x2
9=x2, amiből x=3cm.
A háromszög területe: T=(a*m)/2=3,6*2,4/2=4,32cm2

47b, Deltoid
A négy háromszög mindegyike derékszögű, ezért Pitagorasz-tételét használjuk kétszer:
Először a lenti háromszöget nézve, az oldalai: 4,8cm, 5,2cm és a vízszintes átló fele - jelöljük y-nal. Az átfogó az 5,2cm es oldal.
a2+b2=c2
y2+4,82=5,22, amiből
y2=5,22-4,82
y2=27,04-23,04=4, amiből y=2cm.
A fenti háromszöget nézve, az oldalai: y, x, és 2,5cm (y=2cm). Az átfogó a 2,5cm-es oldal.
a2+b2=c2
22+x2=2,52, amiből
x2=2,52-22
x2=6,25-4=2,25, amiből x=1,5cm.
A deltoid területe: T=e*f/2 (e=2y=4cm, és f=1,5+4,8=6,3)=4*6,3/2=12,6cm2

47c, Szimmetrikus trapéz
Mivel a trapéz szimmetrikus az x-szel jlölt vonalat a másik csúcsnál is meghúzhatjuk. Így kaptunk két derékszögű háromszöge és egy téglalapot. A téglalap vízszintes oldala: 3,5cm, ha ezt levonjuk a 6,5cm-ből a két háromszög víszintes oldalára külön külön 3/2=1,5cm marad. A derékszögű háromszög oldalai, ezek szerint: 1,5cm, x, és 3,9cm. A 3,9cm-es oldal az átfogó.
a2+b2=c2
x2+1,52=3,92, amiből
x2=3,92-1,52
x2=15,21-2,25=12,96, amiből x=3,6cm (ez egyben a trapéz magassága is)
A trapéz területe: T=(a+c)*m/2=(6,5+3,5)*3,6/2=10*1,8=18cm2

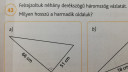
43a, A derékszögű háromszög oldalai: 66cm, 51cm és a keresett harmadik oldal - jelöljük x-szel. Vagyis x az átfogó.
a2+b2=c2
662+512=x2
4356+2601=x2
6957=x2, amiből x=83,4cm