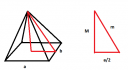Toplista

- betöltés...
Ha szívesen korrepetálnál, hozd létre magántanár profilodat itt.
Ha diák vagy és korrepetálásra van szükséged, akkor regisztrálj be és írd meg itt, hogy milyen tantárgyban!
Téglatest, aköré írt gömb, és abban gúla... mindez egy feladatban
 oroszvirag
kérdése
oroszvirag
kérdése
482
Egy téglatest egy csúcsából kiinduló három élének hossza 8 cm, 10 cm és 14 cm.
a) számítsd ki, hogy a téglatest körülírt gömbjének térfogata hányszorosa a téglatest térfogatának!
A téglatest 10 cm x 14 cm-es lapja egy olyan gúla alapja, amelynek a csúcsa a téglatest szemközti lapjának középpontja.
b) mekkora ennek a gúlának a felszíne?
c) mekkora szöget zárnak be az oldalélei az alaplap síkjával?
d) mekkora szöget zárnak be az oldallapok az alaplap síkjával?
[alapvetően látom magam előtt a térben a testeket, de például nem értem, miből számoljam ki a gömb térfogatát, vagy a gúlában pontosan melyik “belső derékszögeket” kell számolnom és hogyan. Köszönöm a válaszokat!]
a) számítsd ki, hogy a téglatest körülírt gömbjének térfogata hányszorosa a téglatest térfogatának!
A téglatest 10 cm x 14 cm-es lapja egy olyan gúla alapja, amelynek a csúcsa a téglatest szemközti lapjának középpontja.
b) mekkora ennek a gúlának a felszíne?
c) mekkora szöget zárnak be az oldalélei az alaplap síkjával?
d) mekkora szöget zárnak be az oldallapok az alaplap síkjával?
[alapvetően látom magam előtt a térben a testeket, de például nem értem, miből számoljam ki a gömb térfogatát, vagy a gúlában pontosan melyik “belső derékszögeket” kell számolnom és hogyan. Köszönöm a válaszokat!]
Jelenleg 1 felhasználó nézi ezt a kérdést.
0
Középiskola / Matematika
Válaszok
1 velo.gabor
{ Elismert }
megoldása
velo.gabor
{ Elismert }
megoldása
Szia!
a, A téglatest köré írt gömb sugara a téglatest testátlójának fele, azaz r=√ a*a+b*b+c*c /2=√ 8*8+10*10+14*14 /2=√ 64+100+196 /2=9,49cm.
A téglatest térfogata: a*b*c=8*10*14=1120cm3
A gömb térfogata: 4*r3*π/3=4*9,493*3,14/3=3578.21cm3
Vagyis a gömb térfogata 3,2-szerese a téglatestének.
b, A gúla magassága 8cm. A felszín kiszámításához szükségünk van még két adatra a gúlát alkotó két különböző háromszög magasságára. A mellékelt ábrán láthatod hogy ehhez Pitagorasz tételére van szükség.
Az eredeti téglatest alapján a=14cm, b=10cm, c=8cm (ami itt a M-mel egyenlő) keressük a m-et ami a b oldalnál található háromszög magasssága.
Pitagorasz tétellel: 72+82=m2, azaz
49+64=m2
113=m2, amiből m=10.63cm
Vagyis a b oldalnál található háromszög területe: Tb=10*10,63/2=53,15cm2
Az a oldalnál található háromszög magasága Pitagorasz tétellel:
52+82=m2
25*64=m2
89=m2, amiből m=9,43cm
Vagyis az a oldalnál található háromszög területe: Ta=14*9,43/2=66,01cm2
A gúla felszíne: Talap+2Ta+2Tb=14*10+2*53,15+2*66,01=378.32cm2
c, Ehhez a kérdéshez először az alaplap átlóját kell meghatározni Pitagorasz tétellel:
102+142=e2
100+196=e2
296=e2, amiből e=17,2cm
A szöget tangenssel tudjuk meghatározni: tgα=8/17,2=0,465, amiből α=24,94⁰
d, A csatolt ábrán a pirossal jelölt háromszög jobb alsó csúcsánál található szögekre van szükség. Ebből is kettő lesz, mert két különböző háromszög oldalunk van. Viszont mindkét esetben tangenssel számolunk:
tgβ=8/7=1,1428, amiből β=48,81⁰
tgγ=8/5=1,6. amiből γ=57,99⁰
a, A téglatest köré írt gömb sugara a téglatest testátlójának fele, azaz r=√ a*a+b*b+c*c /2=√ 8*8+10*10+14*14 /2=√ 64+100+196 /2=9,49cm.
A téglatest térfogata: a*b*c=8*10*14=1120cm3
A gömb térfogata: 4*r3*π/3=4*9,493*3,14/3=3578.21cm3
Vagyis a gömb térfogata 3,2-szerese a téglatestének.
b, A gúla magassága 8cm. A felszín kiszámításához szükségünk van még két adatra a gúlát alkotó két különböző háromszög magasságára. A mellékelt ábrán láthatod hogy ehhez Pitagorasz tételére van szükség.
Az eredeti téglatest alapján a=14cm, b=10cm, c=8cm (ami itt a M-mel egyenlő) keressük a m-et ami a b oldalnál található háromszög magasssága.
Pitagorasz tétellel: 72+82=m2, azaz
49+64=m2
113=m2, amiből m=10.63cm
Vagyis a b oldalnál található háromszög területe: Tb=10*10,63/2=53,15cm2
Az a oldalnál található háromszög magasága Pitagorasz tétellel:
52+82=m2
25*64=m2
89=m2, amiből m=9,43cm
Vagyis az a oldalnál található háromszög területe: Ta=14*9,43/2=66,01cm2
A gúla felszíne: Talap+2Ta+2Tb=14*10+2*53,15+2*66,01=378.32cm2
c, Ehhez a kérdéshez először az alaplap átlóját kell meghatározni Pitagorasz tétellel:
102+142=e2
100+196=e2
296=e2, amiből e=17,2cm
A szöget tangenssel tudjuk meghatározni: tgα=8/17,2=0,465, amiből α=24,94⁰
d, A csatolt ábrán a pirossal jelölt háromszög jobb alsó csúcsánál található szögekre van szükség. Ebből is kettő lesz, mert két különböző háromszög oldalunk van. Viszont mindkét esetben tangenssel számolunk:
tgβ=8/7=1,1428, amiből β=48,81⁰
tgγ=8/5=1,6. amiből γ=57,99⁰
0
-
oroszvirag: Nagyon szépen köszönöm, ez így teljesen világos! 5 éve 0